[NLP] Longformer: the long-document Transformer
기존 transformer의 input sequence 길이의 한계를 극복하고자 하는 시도인 longformer를 알아봅니다.
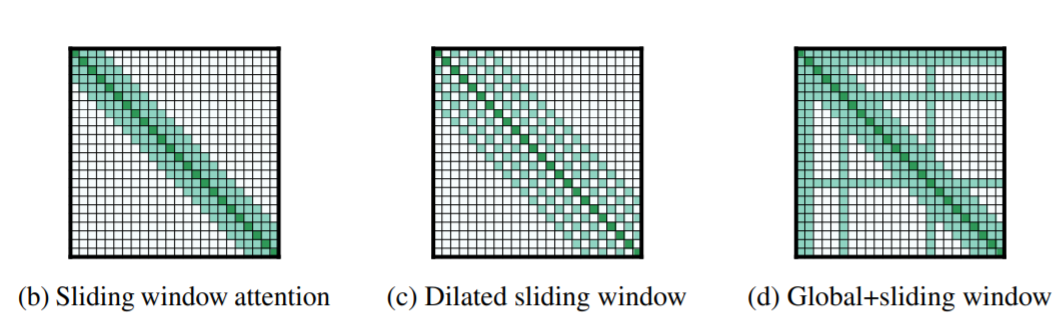
1. Longformer는 기존의 transformer 알고리즘의 $O(n^{2})$ 복잡도를 $O(n)$ 수준으로 낮추어 기존보다 긴 입력 시퀀스를 처리할 수 있는 방법을 제시함
2. 기본적인 아이디어는 MLP의 fully connected한 네트워크의 연산상 비효율성 window를 사용한 CNN으로 극복한 것과 유사
3. 1) Sliding window attention, 2) Dilated sliding window, 3) Global attention을 사용, long document task에서 SOTA를 달성
Contents
- Longformer란?
- Transformer와 Longformer, FCN(Fully Connected Layer)와 CNN(Convolutional Neural Network)
- 3가지 아이디어
- 마치며
Transformer는 NLP를 비롯한 다양한 도메인의 문제를 해결하는 Deep Neural Network에 적용되며 새로운 basic component로 자리잡았습니다. 이러한 추세를 따라 트랜스포머의 장단점을 개선하는 다양한 알고리즘이 앞다퉈 나오고 있습니다. 그 중, 긴 input sequence를 효율적으로 처리하지 못한다는 단점을 보완하고자 하는 Longformer 알고리즘을 소개합니다. 구현체는 여기에서 찾아보실 수 있습니다.
Longformer란?
Longformer는 기존의 트랜스포머의 입력토큰의 한계를 극복하기 위해 고안된 모델입니다. 기존의 트랜스포머는 입력 토큰의 수가 제한되어 있었습니다(일반적으로 512 토큰). 이러한 상황에서 긴 문단을 입력으로 넣어 특정 태스크, 가령 분류를 수행할 경우, 긴 document를 짧은 시퀀스로 쪼개어 입력으로 넣는 방법으로 처리할 수 있습니다.

가령 이 문장 내에서, 사용 가능한 입력값이 1 문장의 길이 정도밖에 되지 않는다고 해봅시다. 이 document를 통째로 넣어서 “$\theta$를 찾아내는 방법론 중 하나는 MLE를 사용하는 것이다” 라는 Question이 주어졌을 때 yes/no를 예측하는 QA 문제를 해결해 보겠습니다. 기존의 트랜스포머를 사용한다면 아래처럼 문장마다 끊어서 입력으로 사용할 수 있을만큼으로 잘라주어 각각 모델에 태워 그 결과를 종합하는 방식으로 해결할 수 있겠습니다.

그러나 이렇게 처리할 경우 개별 chunk 내의 토큰들 사이의 의존성은 반영할 수 없게 됩니다. 즉, 정답의 핵심이 담겨있는 “여기서 어떻게 이 $\theta$를 찾을 수 있을까요?”라는 문장과 “그 방법 중 하나가, MLE를 사용하는 것입니다”라는 문장 내의 토큰 사이의 의존성을 살릴 수 없는 것이지요. 어떻게 하면 이 문제를 해결할 수 있을까요? 긴 문장을 그대로 넣을 수는 없을까요?
Transformer와 Longformer, FCN(Fully Connected Layer)와 CNN(Convolutional Neural Network)
트랜스포머는 key, query 벡터가 각각 길이 d의 시퀀스의 한 유닛마다 존재하면, 각각의 벡터에 대해 내적을 수행해 유사도가 높은 것을 value를 통해 가져오는 구조로 self-attention을 수행합니다. 이 연산을 위해서는 각각의 유닛에 대해 내적을 수행해야하므로 $O(n^{2})$가 됩니다. 이 때문에 전체 긴 문장을 한번에 넣으면 연산 복잡도가 지나치게 커져 학습이 어려워집니다.
이를 극복하기 위해서는, 기존의 뉴럴넷에서 하는 방식을 한번 들여다보면 좋을 것 같습니다. 기존 뉴럴넷에서도 각 레이어마다 $d$개의 유닛이 있으면 $d^{2}$ 만큼의 connection이 생깁니다. 이를 경제적으로 처리하기 위해 Convolution을 사용한 방법이 도입되었습니다. 컨볼루션을 사용하면 길이 3의 window를 사용할 경우 3개의 값을 동시에 보고 그 다음 옆칸으로 슬라이딩 해나가며 웨이트를 계산합니다. 이렇게 되면 $d*k$(k는 window size)가 되므로 $O(d)$로 연산이 상당히 효율적으로 이루어지게 됩니다.
이 방식을 트랜스포머에 적용해보면, Longfomer에서는 sliding window attention이라는 방식을 적용합니다. convolution의 접근은 메모리 상 이점을 취하는 대신에 성능을 일부분 포기하는 방식으로 볼 수 있습니다. 전체를 보는 대신 주변의 몇개만 보기 때문에 레이어 사이의 완전하고 복잡한 연관성 정보를 학습하기는 어렵겠죠. MLP(Multi Layer Perceptron), 달리 말해 FCN은 각 레이어마다 모든 유닛간의 connection을 통해 더욱 복잡한 관계를 더 많은 연산을 통해 학습할 수 있습니다.
그러나 이러한 convolution의 한계는 깊이를 통해 해결될 수 있습니다. 다음 레이어의 유닛에도 똑같이 3 크기의 window의 convolution을 적용하면 이전 레이어의 5개 셀의 정보를 다음 레이어로 전달할 수 있기 때문입니다. 따라서 깊이 쌓으면 쌓을수록 과거 레이어의 전체 셀에 대한 정보를 다음 레이어에 전달할 수 있도록 될테죠.
또한, 개별 토큰의 이웃 지점에 가장 중요한 정보가 있다고, 즉 localized feature가 있다고 가정할 수 있는 경우에 이 방식은 더욱 효율적이리라 기대할 수 있습니다. 가령 이미지의 경우 주변 사물들의 지역적인 특징을 잡아내는 것이 중요하기 때문입니다. 텍스트의 경우에도 어느정도 말이 되는 설명같네요. 주변의 단어가 의미상의 연관이 더 높으리라 생각할 수도 있기 때문입니다.
원래 트랜스포머의 강점은 문장 내의 전체 토큰에 대해 attention을 적용할 수 있다는 점이었습니다. 따라서, Longformer는 CNN이 MLP에게 해결책이 되었던 것처럼 트랜스포머에게 같은 해결책을 제시합니다. 이제 $O(n \times w)$의 복잡도로 같은 연산을 할 수 있을 것입니다. 여기서 w는 window size입니다.
3가지 아이디어
1) Sliding window attention
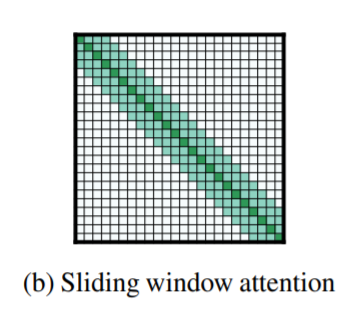
먼저 sliding window attention을 제안합니다. 이는 n번째 토큰에 대해 n-w부터 n+w까지의 토큰에 대해서만 attention을 취해주는 것이죠. 기존의 transformer가 n번째 토큰이 0~d-1번 인덱스의 토큰 전체에 대해 attention을 취해주는 것과는 반대되는 것으로 생각할 수 있습니다. 전부 다 보지 않는다는 것이죠.
2) Dilated sliding window
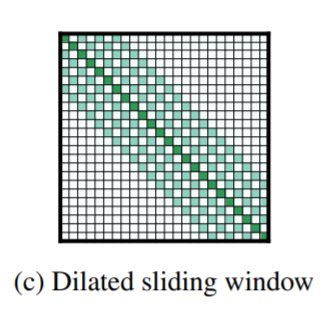
두번째로 dilated sliding window를 보여줍니다. 이는 한칸 너머 한칸 간격으로 어텐션을 취해주는 방식인데, 이를 통해 윈도를 넓힘으로써 더 넓은 구역에 대해 어텐션 해줄 수 있습니다. 이는 레이어에 걸쳐 훨씬 더 빨리 정보를 전달할 수 있다는 것을 의미합니다. 첫번째 방법인 sliding window attention은 local information을 취합하는 데 유용하고, 두번째 방법은 더 global한 정보를 취합하는 데 유용하므로 두번째 방식의 레이어를 모델의 상단에 붙이는 구조를 취하는 것이 나을 것 같습니다.
3) Global attention
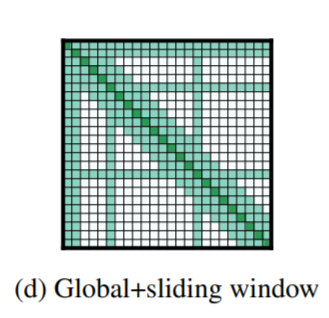
Longformer의 마지막 아이디어는 global attention입니다. 이 어텐션은 sparse한 형태를 띠는데, special token이 몇 개 존재합니다. 이 토큰들은 시퀀스 내 모든 토큰에 대해 attention할 수 있습니다. 마치 Transformer에서 모든 토큰들이 그렇게 하듯이 말입니다. 이들을 특별히 global attention이라 부릅니다. 이들을 어떤 토큰에 대해 수행할지는 해결하고자하는 task에 맞추어 생각해볼 수 있겠습니다.
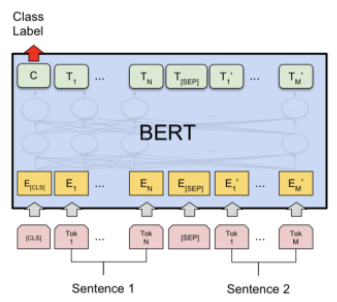
가령 앞서 들었던 예시의 BERT QA 모델에서, 입력으로 [CLS] [query] [SEP] [paragraph]이 있을 때, yes/no로 나오는 binary classification을 수행한다고 해 봅시다. 이 때 최종적으로 사용되는 것은 [CLS] 토큰 뿐이죠. 따라서 이 중요한 토큰은 모든 토큰에 대해 attention을 취하도록 해주는 것이 문제 해결에 유리할 것이라고 생각해볼 수 있겠습니다.
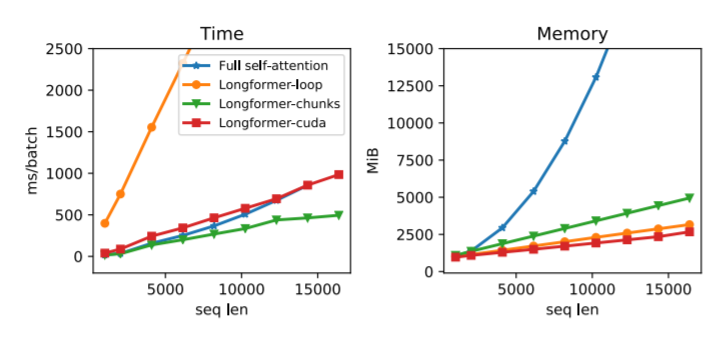
새로운 메모리 소모량은 다음과 같이 계산됩니다.
\[(n*w+s*n*w*2)*L\]
여기서 n은 토큰 수, w는 window, s는 special token 수, L은 레이어의 수를 의미합니다.
계산 복잡도는 따라서 $O(n)$ 으로 기존의 $O(n^{2})$ 에 비해 매우 낮습니다.
마치며
흥미로운 점은, 이들이 실험에 사용한 w 즉 window size가 512라는 것입니다. 이 말은 기존 모델들의 입력 시퀀스의 길이와 동일하다는 것 (!!) 인데요. 즉, sliding window attention 파트에서는 기존의 모든 입력을 받는 것이고 그 이후에 dilated sliding window과 global attention을 사용해 (오바 좀 보태면) 거의 공짜로 훨씬 긴 전체 시퀀스에 대한 정보를 활용해 문제를 해결할 수 있다는 점이 이 논문의 기여라고 볼 수 있겠습니다.
개선을 위한 여러분의 피드백과 제안을 코멘트로 공유해 주세요. 내용에 대한 지적, 혹은 질문을 환영합니다.
출처: https://www.youtube.com/watch?v=_8KNb5iqblE

Leave a comment