[GNN] MAGNN: Metapath Aggregated Graph Neural Network for Heterogeneous Graph Embedding - Paper Review

Graph 분야의 Node Clustering, Node Prediction, Link Prediction task에서 SOTA를 기록한 MAGNN에 대해 알아봅니다.

0. 들어가며

안녕하세요, 배우는 기계 러닝머신입니다!

오늘 살펴볼 논문은 현재 IMBb와 DBLP 데이터 셋의 Node Clustering Task에서 SOTA를 기록하고 있는 MAGNN 알고리즘입니다. 우연히 Metapath 방법론을 접한 뒤로 Heterogeneous Graph Embedding 분야에 대한 논문을 찾던 중 발견한 논문입니다.

해당 논문의 원문은 이 링크에서 확인할 수 있으며, 구현체 역시 깃헙 소스코드로 공개되어 있습니다.

Contents

1. Introduction
2. Graph Embedding의 목적
3. 기존 GNN 방법론과 그 한계
4. MAGNN의 방법론
5. 실험
6. 마무리 지으며

1. Introduction

Introduction

그래프 임베딩은 그래프 데이터 구조에 함축된 비유클리드적인 관계를 포함하여, 노드가 포함하고 있는 복합적인 의미를 수치적인 정보로 나타내고자 하는 방법론입니다. 그런데 현실 세계의 그래프 정보는, 하나 이상의 노드 타입과 관계 타입을 가지고 있는 경우가 많습니다.
이러한 그래프 구성 요소의 다양성을 감안하여 representation을 학습하기 위해서, 이질적인 그래프 임베딩(Heterogeneous Graph Embedding)이라는 개념이 등장했습니다. 이는 단일한 특성을 가지고 있을 것이라 가정하는 동질적 그래프 임베딩(Homogeneous Graph Embedding)과는 상반되는 개념이라고 생각해볼 수 있습니다.

이질적 그래프 임베딩은 그래프의 풍부한 구조적이고 의미론적인 정보를 저차원 공간의 Node Representation으로 임베딩하는 접근법입니다. 현재까지 제안된 모델들은 보통 이러한 이질적인 그래프에 여러 개의 metapath를 정의하여, 복합적인 관계를 파악하고 이웃 선택을 유도하는 방식으로 임베딩을 학습합니다.

그러나, 이러한 기존 모델들은 아래와 같은 한계점을 갖습니다.
1) 노드의 content feature를 생략하거나,
2) metapath 도중의 중간 노드들을 버리거나,
3) 오직 하나의 metapath만을 고려합니다.

이러한 세 가지 한계를 다루기 위해, 최종 성능을 개선하기 위한 MAGNN(Metapath Aggregated Graph Neural Network)이라는 새로운 모델이 제안되었습니다.
이 알고리즘의 세 가지 핵심 구성 요소는 다음과 같습니다.

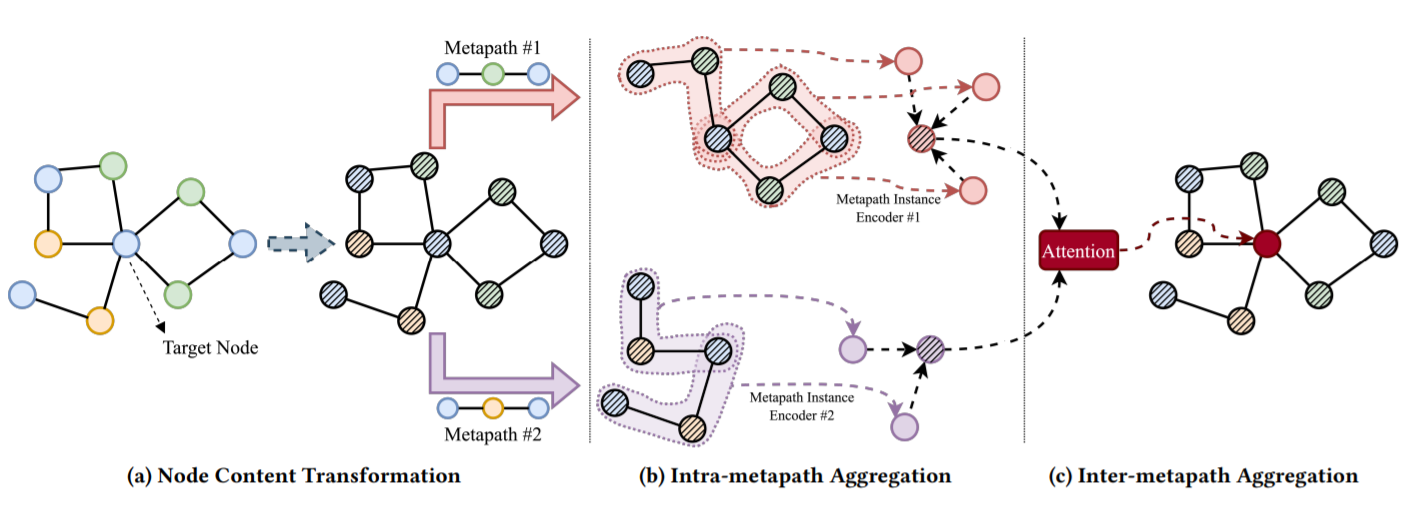
1) 입력 노드 특성(attribute)을 캡슐화하기 위한 content transformation
2) 중간의 의미론적 노드를 통합하기 위한 intra-metapath aggregation
3) 복수의 metapath로부터 오는 메시지를 결합하기 위한 inter-metapath aggregation

이 MAGNN 알고리즘은, node prediction(노드 분류), node clustering(노드 군집화), link prediction(링크 예측) task를 3개의 이질적 그래프 데이터셋을 통해 실험한 결과, 다른 SOTA baseline에 비해 더욱 정확한 예측 결과를 이루어 냈다고 저자들은 주장하고 있습니다.

Graph Embedding의 목적

Graph-Embedding

많은 실제 세계의 데이터는 그래프의 구조로 표현되곤 합니다. 이 그래프는 노드(Node)와 엣지(Edge)로 구성됩니다. 그래프 구조는 분자 구조, social network와 같은 예시를 떠올려 볼 수 있습니다.

여기서 문제는, 그래프의 비 유클리드적인 특성입니다.
우리가 기존의 머신러닝에서는, 유클리드 공간 내에 정의되는 데이터를 주로 다루어 왔습니다. 이미지 데이터, 자연어 데이터 등의 비정형 데이터 역시 유클리드적인 특성을 가정하고 처리해 왔으며, 그러한 접근이 유효했습니다.
하지만 그래프의 경우는 어떨까요?

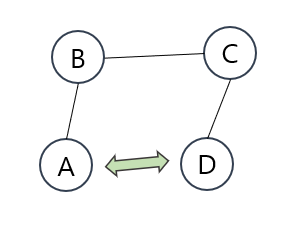
이 그림처럼, 유클리드 공간을 가정했을 때 가장 가까운 노드가 의미적으로는 사실상 가장 먼 노드일 수 있습니다. 따라서 다른 접근이 필요하다는 것이지요.

대부분의 기존 머신러닝 모델에서 사용된 통계기반 모델은 유클리드 공간 내에 고정된 크기의 입력값을 가정합니다.
따라서 그래프의 정보를 저차원의 유클리드 공간 내에 표현해낼 수 있다면 기존의 방법론을 유용하게 사용할 수 있을 것입니다.
이런 목적을 위해, 노드에 대한 저차원 벡터 representation으로 만드는 방법을 그래프 임베딩이라고 합니다. 만약 학습이 성공적으로 이루어져 잘 만들어진 임베딩 벡터를 얻을 수 있다면, downstream task(노드 예측과 같은)에 활용하여 좋은 성능을 얻을 수 있을 것입니다.

3. 기존 GNN 방법론과 그 한계

related works

기존의 방법론은 크게 2가지로 정리할 수 있습니다.
간단히 말하자면, 그래프가 오직 하나의 노드 타입과 엣지 타입을 갖는다고 가정하는 동질적 그래프 가정과 이질적 그래프를 가정하지만 그 학습의 방법론이 적합한 표현 학습에는 불리한 조건을 갖춘, 제한된 이질적 그래프 활용이 바로 그것입니다.

• 동질적 그래프 가정 (Assumption on Homogeneous Graphs)
  -> 모든 노드와 엣지가 하나의 타입만을 갖는다고 가정한 그래프 임베딩 방법론입니다.
  
  

  1. LINE: 노드간의 1계와 2계 근사를 사용해 노드 임베딩을 생성
  2. Random-walk-based method (DeepWalk, node2vec, TADW): Random walk를 기반으로 생성된 노드 sequence를 skip-gram model의 입력으로 사용
  3. Stectral-based GNN(ChebNet, GCN): 전체 그래프의 Fourier domain에서 graph convolution operation을 수행
  4. Spatial-based GNN (GraphSAGE, GAT): 그래프 도메인에 직접적으로 graph convolution 연산을 수행함으로써 spectral-based model의 일반화 및 scalability 문제를 해결.

한계점: 위의 모든 GNN은 동질적 그래프를 위해 고안되었거나, 추천 시스템과 같은 특별한 구조를 갖는 그래프를 위해 설계되었습니다. 대부분의 현존하는 GNN 방법론이 함께 공유된 임베딩 공간 내의 노드의 특성으로 작동하기 때문에, 자연스럽게 노드 특성들이 다른 공간 내에 놓여 있는 이질적 그래프에 적용될 수 없다고 합니다.

• Metapath 방법론
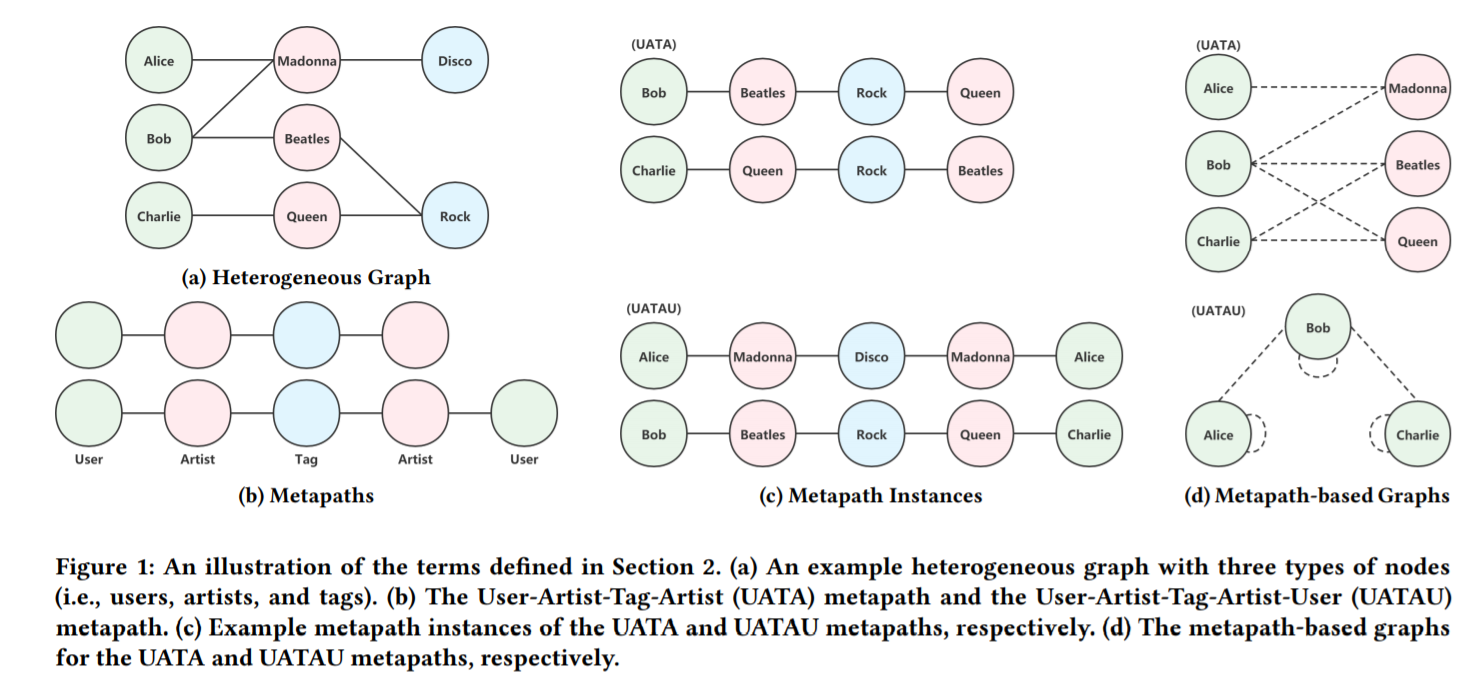
  -> 현재까지 제안된 대부분의 이질적 그래프 임베딩 방법론은 metapath의 아이디어에 기반합니다. 여기서 metapath란, 그래프 내에 그래프 내에 포함된 노드 타입간의 복합적인 관계를 묘사하는, 네트워크 스키마 상에 정의된 엣지 타입과 노드 타입의 정렬된 sequence입니다.
  
  -> 쉽게 말해, 제 인적 네트워크라는 그래프를 가정할 때 “친구-고등학교-친구”와 같은 구조를 metapath라고 한다고 말할 수 있습니다.
  -> 논문의 예시를 따르면, 학술 네트워크에서 저자(Author),논문(Paper),저널(Venue) 세가지의 구성이 있을 때 Author-Paper-Author (APA) and Author-Paper-Venue-Paper-Author(APVPA)는 작가간의 두 종류의 관계를 묘사하는 metapath라고 합니다.
  
  
  1. Metapath2vec: 단일 metapath에 의해 유도되는 random walk를 생성해 skip-gram 모델에 투입해 노드 임베딩을 생성
  2. ESim: 유저가 정의한 metapath가 주어졌을 때, 표집된 긍정/부정 metapath 인스턴스로부터 학습하여 노드 임베딩을 생성
  3. HIN2vec: 복수의 예측학습 task를 수행하여 node와 이질적 그래프의 metapath representation을 학습
  4. HERec: 이질적 그래프를 metapath 이웃에 기반한 동질적 graph로 변환, 그 후 DeepWalk 모델을 적용해 목표 타입의 노드 임베딩을 학습

한계점: 위의 모든 이질적 그래프 임베딩 방법론은 노드 content feature상의 한계를 가지거나, metapath 상의 중간 단계 노드의 정보를 버리거나, 오직 1개 종류의 metapath만들 사용하는 한계가 있습니다.
큰 성능 향상을 보인 것은 사실이지만, 이질적 그래프에서 임베딩된 정보를 더 포괄적으로 활용한다면 좀 더 개선할 수 있는 여지가 있다는 것이 MAGNN이 제안된 배경이라고 할 수 있습니다.

4. MAGNN의 방법론

magnn-approach

MAGNN의 핵심 방법론은, 크게 3가지의 큰 부분으로 이루어져 있습니다.
1) node content transformation
2) intra-metapath aggregation
3) and inter-metapath aggregation

각각 하나씩 살펴보도록 하겠습니다.

• node content transformation
  

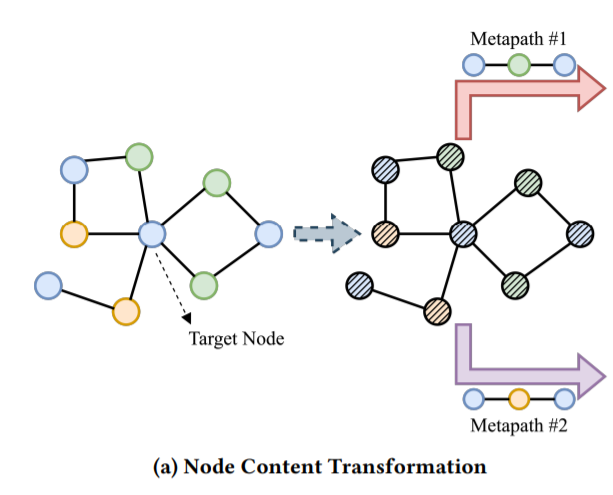
한마디로 표현하자면, 다른 특성을 갖는 노드를 같은 잠재 공간 내로 projection하는 작업이라고 할 수 있습니다.

이질적 그래프에서, 다른 타입을 갖는 노드들은 차원이 다를 수가 있습니다. 뿐만 아니라, 같은 차원을 갖는다고 할지라도 다른 feature space에 놓여 있을 것입니다. 예를 들어 n1차원의 text Bag-of-Words 벡터와 n2차원의 이미지 density histogram 벡터가 있다면, 우연히 n1=n2가 된다고 할지라도 직접적으로 그 둘을 연산할 수 없습니다. 그러므로 이 다른 타입의 노드 피처를 같은 잠재 벡터 공간(latent vector space)내로 projection할 필요가 있는 것입니다.

따라서 노드 벡터를 MAGNN에 넣기 전에, 각 타입의 노드마다 feature 벡터를 같은 latent feature space 내로 projection함으로써 타입에 특화된 linear transformation을 적용합니다.이 작업을 거친 뒤, 모든 노드들의 projection된 feature들은 같은 차원을 공유하게 되고, 이 이후의 작업을 가능하게 합니다.

• Intra-metapath Aggregation (메타패스 내부의 통합)
  

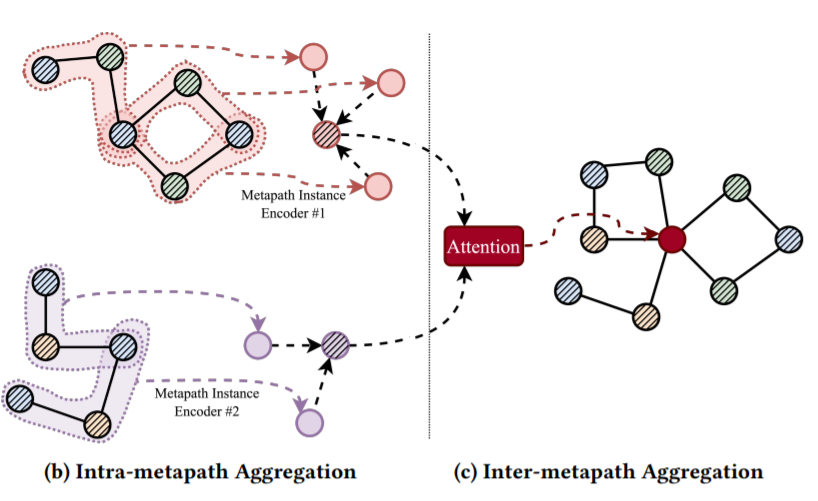
한마디로 표현하자면, metapath의 학습에 사용되는 metapath의 인스턴스들이, 각각 다른 정도로 metapath representation learning에 기여할 것이므로, 이 중요도를 반영해 학습할 수 있도록 만들자는 것입니다.
이 중요도를 학습하는 방식으로는 역시 attention 메커니즘이 활용됩니다.
이러한 방법을 통해, 타겟 노드의 이웃 노드들과 그를 표현하는 metapath context에서 이질적 그래프의 구조적이고 의미론적인 정보를 잡아낼 수 있다고 합니다.

• Inter-metapath Aggregation (메타패스 간 통합)

이렇게 학습한 복수의 개별 metapath의 잠재 벡터들을, 최종 노드 임베딩으로 통합하는 과정입니다.
이 방법으로, 모델은 이질적 그래프 내에 깊이 배여있는 포괄적인 의미를 학습할 수 있다고 합니다.

5. 실험

experiments

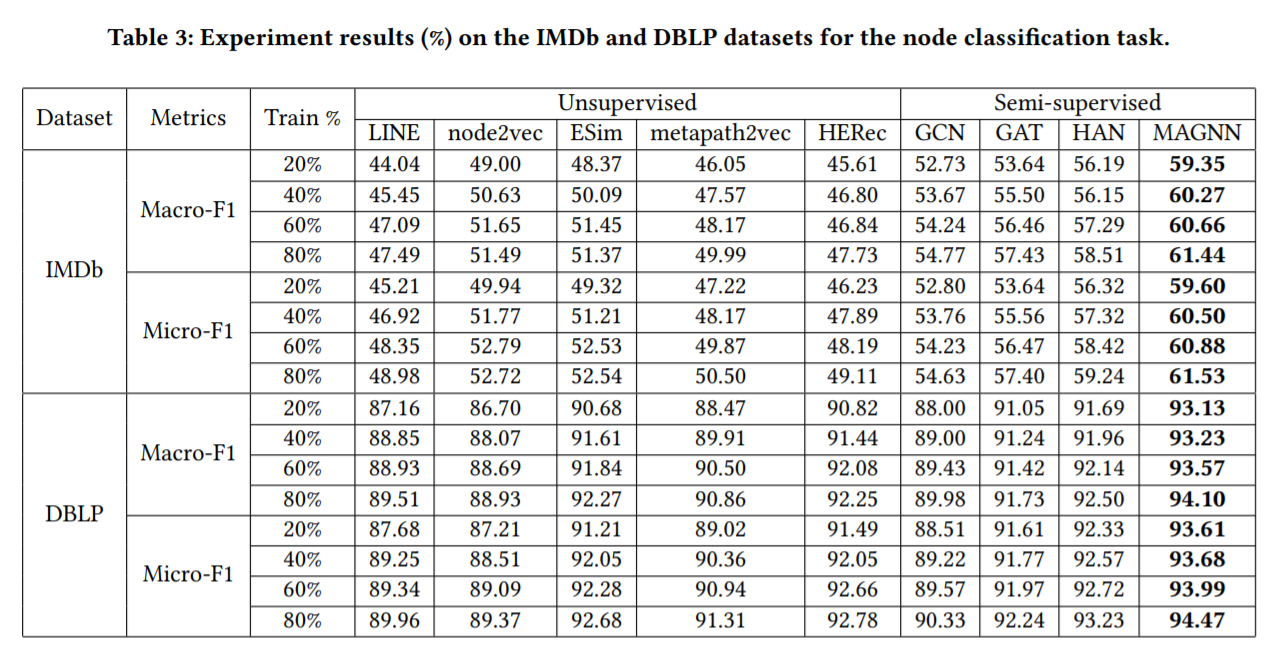
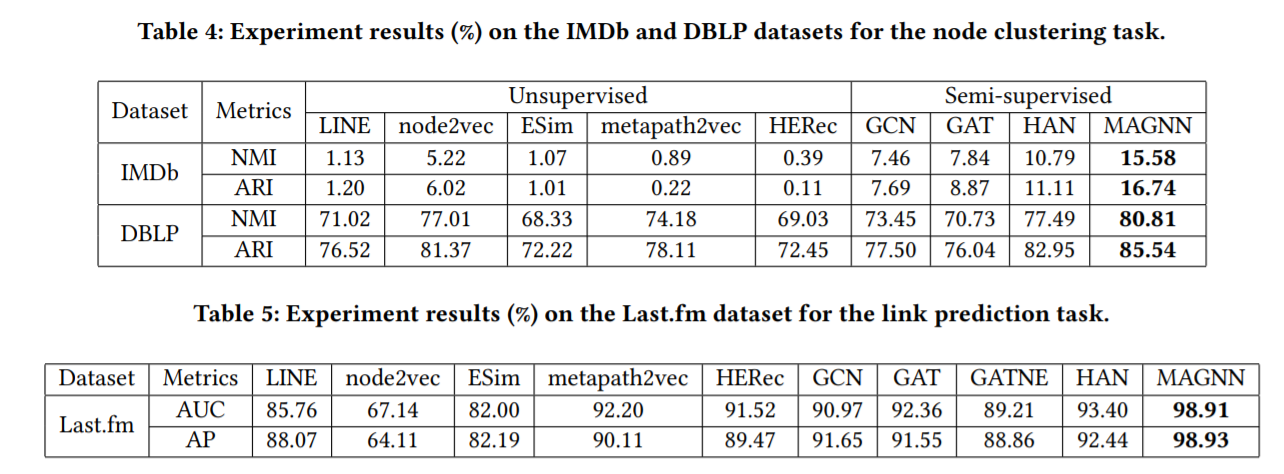
이렇게 학습한 Graph Embedding의 downstream task 성능을 측정하기 위해, IMDb, DBLP, Last.fm 데이터셋에 대해 node prediction(노드 분류), node clustering(노드 군집화), link prediction(링크 예측) task를 수행한 결과, 대부분의 결과가 SOTA를 뛰어넘었다고 합니다.

6. 마무리 지으며

-

여러 한계에도 불구하고, Heterogeneous Graph Embedding에서는 metapath 방법론이 가장 효과적인 접근법으로 여겨지고 있습니다. 직접 metapath를 domain knowledge에 근거해 지정해 주어야하는 현재의 방식을 넘어서 어떻게 더욱 optimal하게 graph representaion을 학습할 수 있을지 궁금해지네요!
여기까지 제 정리였습니다. 논문을 통해 더 자세한 내용을 살펴 보시고, 실제 코드를 실행하며 이해하신다면 더욱 도움이 되리라 믿습니다!
그래프 임베딩에 대한 첫 논문을 다소 advanced paper로 정해 읽으면서도 이해가 많이 부족한 것이 느껴졌습니다. 잘못된 부분이 있거나, 이해가 가지 않는 부분이 있다면 말씀해 주세요! 긴 글 읽어 주셔서 감사합니다.
다음 포스트부터는 조금 더 기초적이고 범용성 있는 그래프 방법론에 대해 다룬 논문을 살펴보려고 합니다. ^^