[General ML Train set] batch 2. 확률과 분포
확률(Probability)과 분포(Distribution)
머신러닝의 관점에서, 확률과 분포가 갖는 의미를 살펴봅니다.

1. 확률(probability)이란, 어떤 사건의 빈도를 나타내는 관점(빈도주의)과 어떤 사건의 발생에 대한 믿음에 의존하는 관점(베이지안) 두 가지가 있다
2. 조건부 확률(conditional probability)이란, 특정 사건의 발생을 전체 사건으로 두고, 그를 전제로 다른 사건이 발생할 확률을 나타낸다
3. 확률 분포(probability distribution)이란, 시행에서 가능한 사건의 부분집합에 대해 확률을 맵핑해주는 함수를 의미한다
Contents
지난 포스트에서는 앞으로 머신러닝의 개념을 이해하기 위해 필요한 MLE와 MAP라는 파라미터 최적화 방법에 대해서 배워보았습니다. 이번 시간에는, 머신러닝을 위한 기초적인 확률과 통계에 대한 개념, 그리고 여러가지 자주 쓰이는 분포에 대해서 알아보겠습니다.
확률(Probability)이란?
확률이란 개념에 대해 다양한 철학적 논의가 존재합니다. 때문에 정확한 정의를 내리는 것은 어렵지만, 여기서는 활용할 수 있을 정도의 정의를 내리려고 합니다.
먼저 철학적으로 살펴보면, 다음 두 가지 중의 하나의 맥락에서 쓰입니다.
1) 객관론자(objectrivists)는 사건들의 상태를 묘사하기 위해 수를 할당하는데, 이를 확률로 나타냅니다. 즉, 여기서는 counting의 개념으로 쓰입니다.
2) 주관론자(subjectivists)는 사건들에 대한 자기 자신의 고유한 믿음에 대해 수를 할당하는데, 이를 확률로 나타냅니다. 여기서는 betting의 개념이라고 볼 수 있습니다.
수학적으로 살펴볼까요?
수학적으로는, 다음의 특징들을 만족하는 함수를 의미합니다.
$P(E) ∊ R$, $P(E)≥0$, $P(\Omega)=1$
풀이하자면, P(E)는 E라는 사건이 발생할 확률의 함수 값은 실수 집합의 원소임을 나타내며, 0 이상의 값을 갖는다는 것을 의미합니다. 또, $\Omega$로 표현되는 전사건(total event)의 확률은 1을 의미합니다. 전사건은 전체사건을 뜻하는 말입니다. 이 세상의 모든 삼라만상의 사건을 한데 어울러 이들이 발생할 확률은 1이겠지요.
$P(E_1∪E_2∪ …) = \sum_{i=1}^∞ P(E_i)$
상호 배제적인(mutually exclusive) 사건의 시퀀스가 있을 때, 이 사건들의 합집합의 확률은 개별 확률을 각각 더해준 값과 동일하다는 의미입니다.
이러한 확률은, 잘 알려져 있듯이 다음과 같은 특성을 갖습니다.
- if $A ⊆ B$ then $P(A) ≤P(B)$
- $P(∅) = 0$
- $ 0 ≤ P(E) ≤1$
- $P(A∪B) = P(A) + P(B) - P(A∩B)$
- $P(E^C)=1-P(E)$
조건부 확률
앞서서 전사건을 살펴보았습니다. 그렇지만, 때때로 전체 사건을 살펴보는 것이 아니라 특정 조건이 주어졌을 경우를 생각해보는 것이 필요할 때가 있을 것 같네요.
- 이번에 성과급을 1,000만원을 받으면 아내가 절반 이상 가져갈 확률은?
- 아이스크림을 남겨두고 등교했을 경우 누나가 다 먹었을 확률은?
- 모델 파라미터가 X일 경우, Y 값이 나올 확률은?
위의 사례는 특정 사건이 발생했을 경우를 전제로 하여 다른 사건이 발생할 확률에 대해 물음을 하고 있습니다. 이런 표현을 수학적으로 나타내기 위해, 우리는 조건부 확률이라는 개념을 사용할 수 있겠습니다. 수식으로 한번 살펴보겠습니다. 아마도 낯이 익는 수식일 것입니다.
$P(A \mid B) = \frac{P(A∩B)}{P(B)}$
이는 B 사건이 주어졌을 때 (given B) A 사건이 발생할 확률을 나타냅니다. 달리 표현하면,
$Posterior = \frac{Likelihood * Prior Knowledge}{Normalizing Constant}$
즉 사후 확률은 우도와 사전확률을 곱한 뒤 B 사건의 발생 확률로 나누어 준 것이 되겠습니다. 이 수식은 앞으로도 매우 중요하게 다루어질 예정입니다.
여기서, 이 공식의 몇 가지 유용한 변형을 살펴보고 가겠습니다.
$P(B \mid A) = \frac{P(A \mid B)P(B)}{P(A)}$
앞서 살펴본 식은 B 사건이 주어졌을 경우 A 사건의 발생 확률이었는데, 여기서는 A 사건이 주어졌을 경우 B 사건의 발생 확률에 대한 수식으로 바꾸어 표현하게 되었네요. 달리 말해 조건 사건과 목표 사건을 바꾸어 나타낼 수 있다는 것입니다.
한가지 더 살펴 보겠습니다.
$P(A) = \sum_{n}P(A \mid B_n)P(B_n)$
이는 우리의 목표 사건인 A의 발생 확률을 모~든 조건 B들에 대한 조건부 확률과 사전확률을 더해줌으로써 구할 수 있다는 것을 나타냅니다.
확률 분포(Probability Distribution)란?
확률 분포란, 하나의 사건을 특정 확률로 맵핑시켜주는 함수를 의미합니다. 여기서 사건은 우리가 흔히 통계학에서 다루는 연속적 수치 변수가 될 수도 있고, 이산적 범주형 변수가 될 수도 있습니다.
확률 분포는 무작위적 시행/실험/설문 등에서 발생할 수 있는 잠재적인 사건의 부분집합에 대해 하나의 확률을 할당해주게 됩니다.
가령 두 개의 주사위를 굴리는 무작위적 시행이 있을 때, 각각의 눈의 합이 가질 수 있는 값 (2~12 사이의 값)이 각각의 확률에 맵핑되겠죠.

| 사건 (두 주사위의 합) | 확률 | percentage |
|---|---|---|
| 2 | 1/36 | 3% |
| 3 | 2/36 | 6% |
| 4 | 3/36 | 8% |
| 5 | 4/36 | 11% |
| 6 | 5/36 | 14% |
| … | … | … |
| 12 | 1/36 | 3% |
| 12 | 1/36 | 3% |
이 표와 같이 사건->확률값으로 맵핑해주는 그 함수가 바로 확률 분포가 되겠습니다.
여러가지 확률 분포들
만약 특정 확률 분포에 대해서 잘 알려져 있다면, 우리는 실제 세계에서 일어나는 다양한 사건들에 대해 여러가지 가정을 붙임으로써 해당 분포를 따른다고 상정하고, 그 분포에 대해 알려진 여러 특성을 활용해서 우리가 풀고자 하는 문제들을 해결할 수 있을 것입니다.
가령 100개의 휴대폰에 1개의 비율로 불량품이 포함되어 있다고 할 때, 상품 박스 100개를 뽑아서 검사해 봤을 때 불량품이 1개, 혹은 2개가 포함될 확률을 계산하고 싶다고 해보면, 이러한 사건이 포아송 분포를 따른다고 가정한 뒤 계산할 수 있을 것입니다.
여기서는, 널리 알려져 자주 활용되는 여러 확률분포에 대해 살펴보려고 합니다.
1. 정규분포 (Normal Distribution, Gaussian Distribution)
정규분포는, 이름에서 알 수 있듯이 매우 널리 관측되는 분포입니다. 정규분포는 연속형 수치 변수에 대한 분포(즉 연속확률분포)이며, 유명한 수학자 가우스의 이름을 따 가우시안 분포라고 부르기도 합니다.
(통계를 처음 배울 때, 교수님이 normal distribution이라고 설명하시다가, gaussian distribution이라는 용어를 사용하시기에 혼란에 빠졌던 기억이 납니다..ㅎㅎ)
정규분포는 일상에서 매우 흔하게 찾아볼 수 있는데요. 가령 전체 부서 남자 직원의 키를 조사해볼 때, 평균값 주변에 상대적으로 많이 분포해 있고, 평균에서 멀어질수록 더 적은 수가 분포되어 있는 등의 예시를 떠올릴 수 있겠네요.
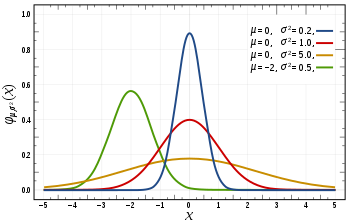
정규분포는 두개의 파라미터(모수, parameter)를 갖습니다. 바로 $\mu$와 $\sigma$인데요. 각각 평균과 분산을 나타내는 파라미터로, 평균은 위의 그림에서 볼 수 있듯이 ‘중심이 어디에 있는가’를 조절하며, 분산은 ‘중심으로부터 얼마나 퍼져 있는가’를 조절해 줍니다.
정규분포의 수식은 다음과 같습니다.
$f(x; \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
일반적으로는 $N(\mu, \sigma^2)$로 표기합니다.
- Mean : $\mu$
- Variance : $\sigma^2$
2. 베타 분포(Beta Distribution)
두 번째로 살펴볼 베타분포는, 0~1 사이의 닫힌 구간 내에서 연속적인 값을 갖는 분포입니다. 이 분포는 매우 유용한 성질을 가지고 있는데요, 그 이유는 베타 분포가 확률의 특성과 잘 들어맞아 확률을 나타내기에 용이하기 때문입니다.
베타 분포의 수식은 다음과 같습니다. 베타 분포 역시 2개의 파라미터, $\alpha, \beta$를 가지며, 이들에 의해 평균과 분산이 정의됩니다.
$f(\theta; \alpha, \beta ) = \frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)}$, $B(\alpha,\beta) = \frac{\gamma(\alpha)\gamma(\beta)}{\gamma(\alpha+\beta)}, \gamma(\alpha)=(\alpha-1)!, \alpha ∈ N^+$
일반적으로 $Beta(\alpha, \beta)$로 표기합니다.
- Mean : $\frac{\alpha}{\alpha+\beta}$
- Variance : $\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$
3. 이항 분포(Binomial Distribution, Bernoulli Distribution)
세 번째로 살펴볼 분포는 이항 분포인데요. 이항 분포는 이산적 수치형 변수를 다루는 이항확률분포 중 가장 단순한 형태입니다. 가장 간단한 예시는, 지난 시간에 살펴본 압정 던지기 문제인데요. 0 혹은 1이 나오는 단순한 형태의 시행을 Bernoulli trial (버눌리 시행, 혹은 베르누이 시행이라 읽습니다)이라고 합니다.
이항 분포의 수식은 다음과 같습니다.
$f(\theta; n, p) = \left(\begin{array}{c}n\ k\end{array}\right) p^k (1-p)^{n-k}, \left(\begin{array}{c}n\ k\end{array}\right) = \frac{n!}{k!(n-k)!} $
표기법은 $B(n,p)$ 입니다.
- Mean: $np$
- Variance: $np(1-p)$
역시 n,p라는 파라미터로 평균과 분산을 구할 수 있습니다.
4. 다항 분포(Multinomial Distribution)
마지막으로 살펴볼 분포는 다항분포입니다. 다항분포는 이항분포의 일반화된 버전으로, discrete한 다양한 사건에 대한 분포를 나타냅니다. 가까운 예시로는 문장 내의 단어 선택이 있겠습니다. 가령 I love apple cookie more than apple phone. 이라는 문장이 있을 때, apple 외의 모든 단어는 1회 등장한 반면 apple 이라는 단어는 2번 등장한 것을 나타낼 때 다항분포를 사용할 수 있습니다.
수식은 다음과 같습니다.
$f(x_1, … , x_k; n, p_1, …, p_k)= \frac{n!}{x!…x_k!}p_1^{x_1}…p_k^{x_k}$
표기법은 $Mult(P), P=<p_1,…,p_k>$ 입니다.
- Mean: $E(x_i) = np_i$
- Variance: $Var(x_i) = np_i(1-p_i)$
닫으며
지금까지 간단한 확률과 분포에 대해 알아보았습니다.
개선을 위한 여러분의 피드백과 제안을 코멘트로 공유해 주세요. 내용에 대한 지적, 혹은 질문을 환영합니다.
해당 포스트는 카이스트 문일철 교수님의 동의를 얻고, 강좌 내용과 자료, 그리고 reference의 자료를 참고하여 작성되었습니다. 원 강좌는 여기에서 보실 수 있습니다.
자료 공유를 허락해 주신 문일철 교수님께 감사의 말씀을 전합니다.

Leave a comment