[Deep Learning] 비선형 함수를 사용하는 이유에 대한 시각적 설명
신경망 모델에서 비선형 활성화함수를 사용하는 이유에 대한 두 가지 접근을 알아봅니다.
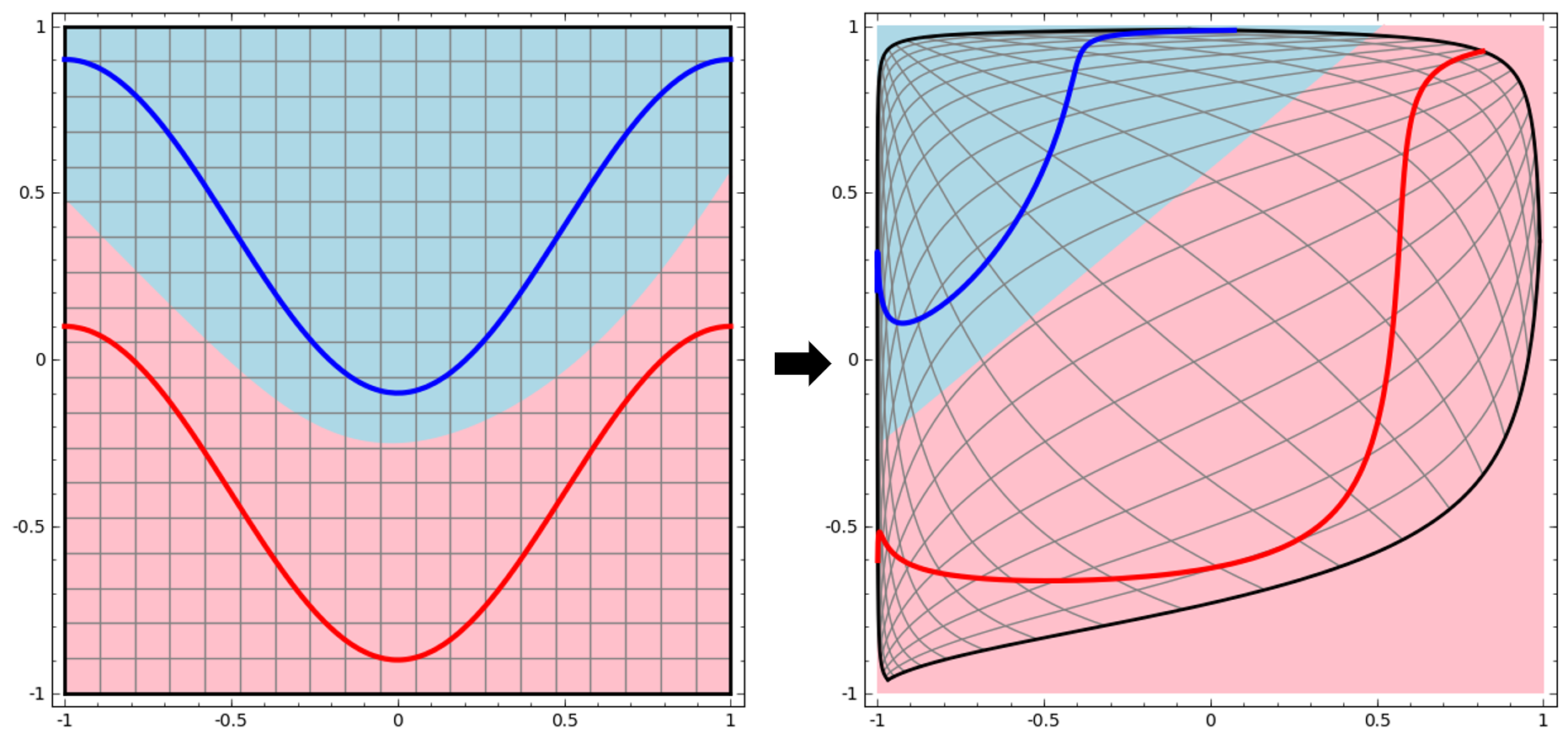
뉴럴 네트워크는, 사실상 매 레이어마다 입력 공간(input space)를 왜곡하여 새로운 피처를 만든다!
안녕하세요, 오늘은 신경망 모델에서 비선형 활성화함수(non-linear activation function)을 사용하는 이유에 대해 간단히 정리해 보려 합니다.
1. XOR 문제 해결
먼저, 일반적인 설명으로는 출력 값을 비선형적으로 만듦으로써 XOR 문제를 해결하기 위함이라는 것입니다.
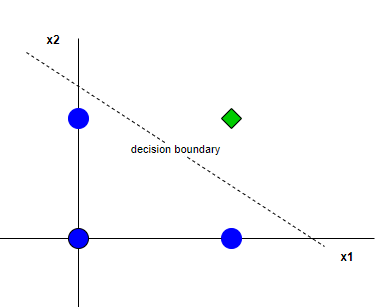
아래의 형태로 구성된 문제는 AND 문제입니다.
x1과 x2가 모두 1인 녀석만 yes로 라벨을 붙이는 문제이지요.
이 경우에는 결정경계를 단순히 직선 하나만 그어 주어도 충분합니다.
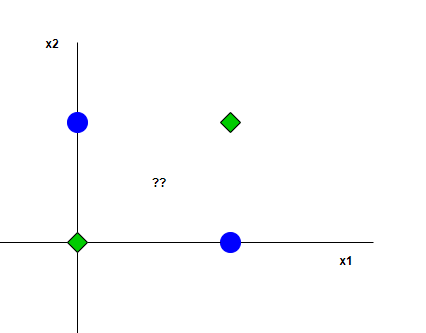
하지만 아래의 형태를 가지는 XOR 문제에서는 직선으로 문제를 해결할 수 없습니다.
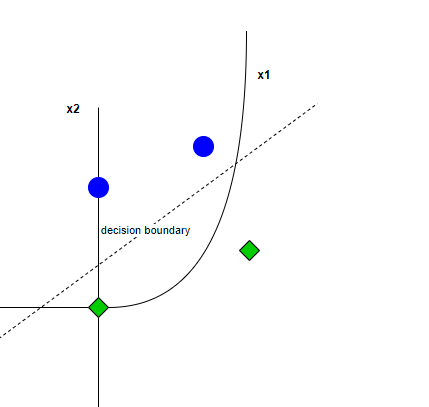
이러한 문제를 해결하기 위해, 비선형 활성화함수를 통과시킨 결과값을 사용하면
출력이 입력값의 선형결합으로 복제될 수 없는 형태로 (비선형성) 나오게 되고,
XOR을 비롯한 복잡한 문제를 해결할 수 있게 됩니다.
비선형 함수가 없이 뉴럴 네트워크의 레이어를 중첩하는 것은 단순히 선형결합이 반복되는 것이고,
때문에 하나의 함수만으로 근사하는 것과 유사해져 중첩해서 쌓는 이점을 잃게 됩니다.
2. 입력 피처의 왜곡
1번의 해석은 이미 많은 자료에서 이야기하고 있기에, 이 2번 해석이 더 재미있어 보입니다.
뉴럴넷은 입력 공간을 왜곡하여, 새로운 피처를 만들어 냅니다. 입력값을 ax+b의 형태로 통과한 뒤, 활성화함수를 통해 나온 결과를 출력으로 뱉습니다.
이 결과 새로운 feature space가 만들어집니다.
이 때 비선형 활성화함수의 가치가 드러납니다.
비선형 함수들은 타겟 함수의 곡률(curvature)을 바꿀 수 있게 해줌으로써, 이후의 레이어에서 선형으로 분리할 수 있도록 만들어줍니다.

즉, 왼쪽 그림에서는 곡선으로 만들어졌던 결정경계가, 비선형 활성화함수를 통과한 뒤 왜곡된 공간 내에서는 아래와 같이 선형으로 구획할 수 있게 된 것입니다.
개선을 위한 여러분의 피드백과 제안을 코멘트로 공유해 주세요.
내용에 대한 지적, 혹은 질문을 환영합니다.
참고: https://colah.github.io/posts/2014-03-NN-Manifolds-Topology/
https://cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html
https://stackoverflow.com/questions/26454357/graphically-how-does-the-non-linear-activation-function-project-the-input-onto#new-answer

Leave a comment