[RecSys] Multi-Armed Bandits
최대의 이득을 찾는 전략을 학습하는 강화학습 방식의 추천 알고리즘인 MAB에 대해 살펴 봅니다.
어떤 슬롯머신이 어떤 수익률을 가지는지 모를 때,
탐색(Exploration)과 활용(Exploitation)을 적절히 사용하여
최적의 수익을 찾아내고자 하는 강화학습 알고리즘!
1. MAB(Multi-Armed Bandits)란, 여러 선택지가 있을 때 어떤 선택이 가장 큰 보상을 얻을 수 있을지 모를 때 최적의 전략을 세우기 위한 알고리즘
2. 아직 잘 모르는 선택지를 시도해보는 탐험(Exploration)과, 높은 보상을 얻을 수 있다고 알려진 선택지를 선택하는 활용(Exploitation)을 적절히 활용해야함
3. 이러한 탐험과 활용 사이를 잘 조정하기 위해, $\epsilon$-greedy, UCB(Upper Confidence Bound) 등의 다양한 variant가 고안되었음
Contents
1. Multi-Armed Bandits이란?
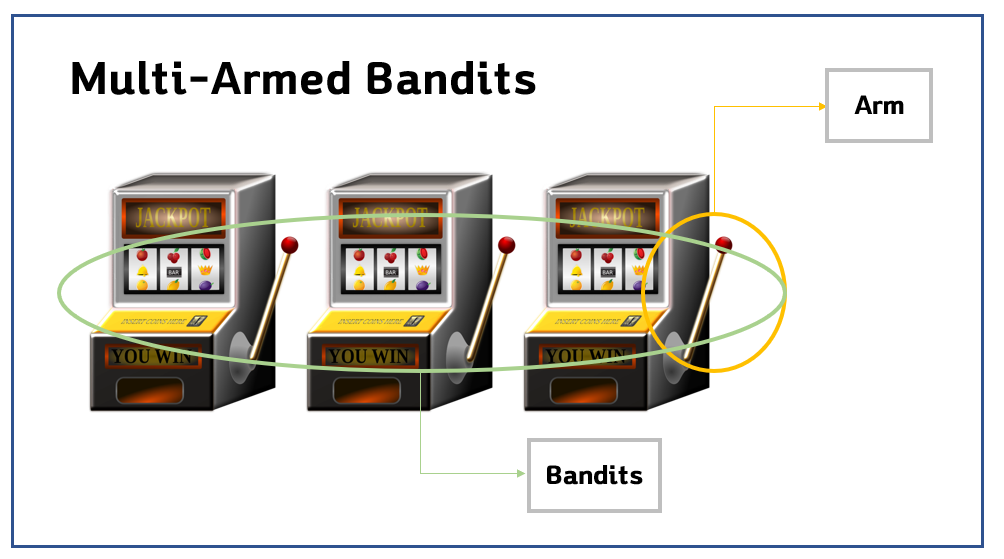
Multi-Armed Bandits은, 여러개(Multi)의 레버(Arm)를 가진 여러대의 슬롯머신(Bandits)이라는 뜻입니다.
이 알고리즘의 유래가, 과거 카지노에서 어떤 슬롯머신에 게임을 해야 최대한 많은 수익을 얻어낼 수 있을까? 하는 고민에서 출발했기 때문이라고 합니다.
조금 더 기술적으로 정의하자면, 아래 세 가지의 제약이 모두 주어졌을 때의 문제 (multi-armed bandit problem)를 해결하는 알고리즘입니다.
1) 한정된 자원 상황 하에 여러 개의 상충하는 선택을 내려야하는 경우
2) 어떠한 선택이 얼마 만큼의 이득을 얼마 만큼의 편차로 제공하는지를 알 수 없을 때 (그러나 같은 선택을 여러번 내림에 따라 불확실성이 줄어들 때)
3) 이 선택들의 예상되는 최대 이득이 극대화되도록 하고자 할 때
이제부터는, 우리의 타짜 철용좌가 자신의 마지막 승부를 거는 상황을 예시로 들어 더욱 쉬운 말로 설명해 보고자 합니다.
2. 예시 상황

무너진 줄만 알았던 마포대교를 무사히 건넌 철용좌는 마지막 재산 1,000만원을 끌어 안고 인근의 유명한 도박장에 도착했습니다. 3대의 슬롯머신이 눈 앞에 놓여있고, 기계마다 수익률이 다르게 책정되어 있다는 사실을 알게 됩니다. 여기서 우리의 철용좌가 재기를 위해 최대한의 이익을 낼 수 있는 방법은 무엇일까요?
여기서 철용좌는 아직 3개의 bandit의 보상을 전혀 알지 못합니다. 철용좌는 마지막 자존심을 되찾을 수 있을까요?

평소 머신러닝에 관심이 많던 철용좌는 이 마지막 기회를 최대한 살리기 위해, 강화학습의 기초적인 형태인 Multi-Armed Bandit 알고리즘을 적용해보고자 합니다. 그가 떠올린 기초적인 강화학습의 플로우는 다음과 같습니다. 일반적인 강화학습과는 달리, 환경이 변하지 않는다는 점에서 더욱 문제가 단순해졌습니다.
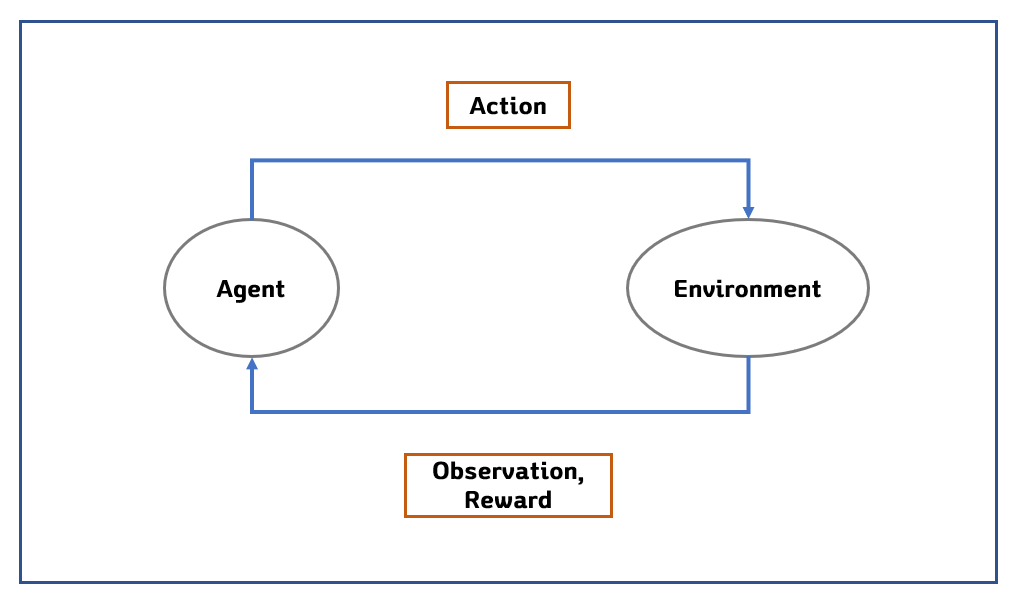
여기에서 Agent는 우리의 강화학습 모델입니다. 이 Agent가 어떠한 액션(예를 들면, 버튼 2번을 누른다!)을 취하면, Environment(환경)은 우리에게 어떠한 보상을 주게 됩니다.
간단히 말해서, Agent가 선택을 잘 했으면 “잘했어~”하고 칭찬 해주고,
반대로 잘못된 선택을 하면 “응, 왜 그거 골랐어~” 하고 혼내주는 것이지요.
이러한 과정 끝에, Agent는 최종 시점에서 최대의 누적 수익을 얻기위해 자신의 전략(Policy)을 점점 수정해 나가고, 이러한 플로우가 잘 구성되어 있는 경우에 최적의 전략을 발견하면서 학습을 종료하게 됩니다.
앞서 말했던 칭찬과 면박은 각각 Reward의 수치값으로 표현됩니다. 잘했어~ 는 돈을 더 주는 것이고, 못했어~는 돈을 잃게 만드는 것이지요.
여기서 보상은 두 가지의 형태를 가질 수 있을 것입니다.
1) 일정한 보상 (Stationary Reward)
만약 보상이 일정하다면 문제는 아주 간단하겠지요? 가령,
- ① 번 버튼은 500원,
- ② 번 버튼은 100원,
- ③ 번 버튼은 -1000원이라고 해봅시다.
그렇다면 몇번의 탐색 끝에 ① 번 버튼이 최고라는 것을 알게 될 것이고, 우리의 Agent는 ① 번을 남은 기회동안 눌러 최대의 보상을 얻게 될 것입니다.
2) 변칙적인 보상 (Non-Stationary Reward)
하지만 현실은 역시 녹록치 않죠.
- ① 번 버튼의 보상은 첫 회에 500원이었다가 시간이 흐름에 따라 한 회마다 -50원씩 줄어듦
- ② 번 버튼은 100원이었다가 -10원, +20원, -30원, +40원…
- ③ 번 버튼은 -1000원에서 한 회마다 500원씩 늘어남
이렇게 다양한 방식으로 보상이 변화할 수도 있을 것 같습니다. 이러한 상황을 변칙적인 보상(Non-Stationary Reward)라고 합니다.
멋진 말로, 보상의 분포가 시간의 흐름에 따라 변화한다고 표현합니다. (Reward distribution changes over time)
이 경우에는 조금 더 복잡한 접근이 필요하겠죠?
어떻게하면 이렇게 알 수 없는 보상을 정확히, 최소한의 손실로 알아낼 수 있을까요? 이를 위해, 탐색과 활용(Exploration and Exploitation) 전략을 취하게 됩니다.
3. 탐색과 활용 (Exploration & Exploitation)
우리의 철용좌는 단 1,000번 만을 시도할 돈만 가지고 있기 때문에, 제한된 기회 내에서 최대한의 수익을 얻어내야 합니다.
그런데, 3개 중 1개의 가장 우수한 수익을 주는 슬롯머신이 있다고 할 때,
- 3개 중 어떤 슬롯이 가장 많은 이득을 줄 지 알 수 없는 상황에서 한가지에 모두 쏟아버리기에는 위험할 것 같고(exploitation only),
- 또 반대로 계속 3개를 골고루 골라버리기에는 최대의 이득을 못 누릴 것 같습니다. (exploration only)
여기서, 두 번째 전략을 탐험(Exploration), 첫 번째 전략을 활용(Exploitation) 이라고 합니다. 직관적으로는 다음과 같은 의미를 갖습니다.
1) 탐험(Exploration): 어떤 버튼이 얼마의 보상을 주는지 탐험해보기
2) 활용(Exploitation): 알아낸 보상을 바탕으로 돈을 뽑아먹기
이 두 가지 전략을 적절히 섞어서 쓰는 것이 필요할텐데, 어떻게 풀어낼 수 있을까요? 이제 그 방법에 대해 알아보겠습니다.
4. 보상 최대화 알고리즘
탐색과 활용을 잘 절충해서, 보상을 최대화하는 세 가지 접근법에 대해 배워보겠습니다.
4-1. Greedy 알고리즘
그게 좋단 말이지? 묻고 더블로 가!
다시 철용좌의 이야기로 돌아가 봅시다. 1,000번에 걸쳐 슬롯을 돌려 볼 돈이 있을 때, 30번 정도를 ① ② ③ 번 버튼에 각각 10번씩 투자한 결과가 다음과 같다고 합시다.

이럴 때, 오케이, ① 번으로 나머지 970번 가즈아!

하는게 Greedy 알고리즘이라고 할 수 있겠습니다.
가장 수익이 잘 나오는 버튼을 “탐욕적으로(greedy)” 소비하는 알고리즘이라 greedy라는 이름이 붙은듯합니다.
이를 수식으로 표현하면 아래와 같습니다!
$q_*(a) \doteq \mathbb{E}[R_t \mid A_t = a] . $
먼저 위의 식에서, $q_*(a)$는 $a$라는 임의의 버튼을 눌렀을 때 얻는 기대 보상입니다.
등호 위에 점이 하나 찍혀 있는 것은 “거의 같다” 라는 의미이구요 (is defined as),
저 두꺼운 E ($\mathbb{E}$) 는 기댓값을 나타내고, 그 안의 내용은 “$t$ 시점에서 $A$(선택할 버튼, Action) 이 $a$ 라는 버튼일 때의 $R$(보상, Reward)”
이라는 의미입니다.
요약하자면 $q_*(a)$는 $a$를 골랐을 때 $t$ 시점에서 얻을 기대 보상이라는 뜻인데요.
그런데 현실에서는 $q_*(a)$를 알지 못하기 때문에, 이를 추정한 $Q_t(a)$를 사용한다는 것입니다.

이 식은 이 $Q_t(a)$를 추정하는 방법을 보여줍니다.
$t$기는 현재의 시점, a는 우리가 고른 버튼, $Q_t(a)$는 $t$ 시점의 $a$ 버튼의 진짜 보상의 추정치를 의미합니다.
맨 오른쪽 식의 1 모양은 Indicator Function이라고 하는데요.
이는 $A_i$가 $a$라는 식이 성립할 때 1의 값을, 그렇지 않을 때 0의 값을 출력하는 함수입니다.
ㅎㅎ 말이 정말 길죠. 정리하자면,
분모는 “$t$기 전까지 $a$가 선택된 횟수의 총 합”을, 분자는 “$t$기 전까지 $a$가 선택되었을 때 보상의 총 합”을 의미합니다.
쉽게 말해 $a$가 뽑혔을 때 보상을 평균 내준 이 값을, $a$의 진짜 보상값일거야! 라고 가정하는 것이 됩니다.
거의 다 왔습니다.
Greedy 방식은 다음과 같은 방법으로 Action을 선택합니다.
$A_t \doteq argmax_a Q_t(a)$
이 식은, 우리가 선택할 Action(즉, 어떤 버튼을 선택하는지)은 아까 구한 $Q_t(a)$를 최대로 만들어 주는 $a$를 사용한다! 라는 말입니다.
4-2. $ \epsilon $ - Greedy 알고리즘
묻고 더블로 가! 긴 하는데 가끔씩 살펴보긴 하자.
얼핏 보기에도 철용이형의 Greedy 알고리즘 방식은 돈을 잃기 쉬워보입니다. 단순히 30번의 시도로 확신을 해버린다는게 문제인데요.
$\epsilon$ (앱실론) - Greedy 알고리즘은, 이러한 문제를 조금 보완해 줍니다.
매 번마다 동전을 던져서, 앞면이 나오면 새로운 버튼을 눌러보고, 그렇지 않으면 지금까지 나온 최적의 버튼을 누르는 결정을 한다는 겁니다.
여기서 $\epsilon$은 동전을 던졌을 때 앞면이 나올 확률이라고 생각할 수 있습니다.
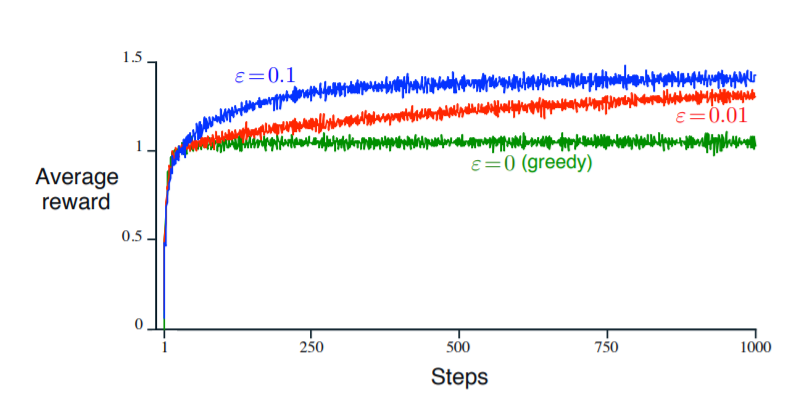
이런 약간의 변칙을 사용함으로써, greedy 방식(녹색 그래프)에 비해 더 나은 결과를 낳는다고 합니다.
(+) 변칙적인 보상을 가질 때 더욱 효율적인 e-greedy 알고리즘 적용을 위해, 다음과 같은 방식이 적용되었습니다.
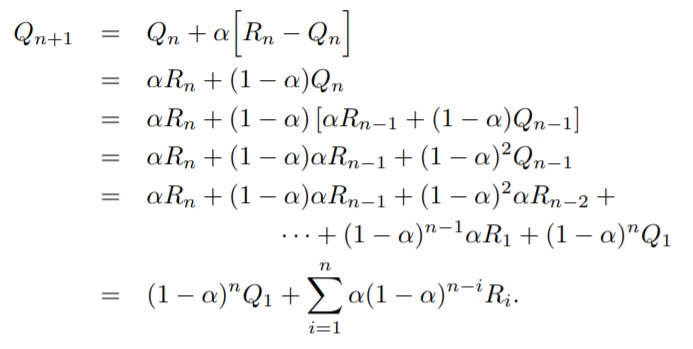
exponential decay를 적용한 것을 알 수 있습니다.
4-3. UCB(Upper-Confidence-Bound) 알고리즘
아직 안 살펴 본 애들을 좀 더 보면서 가자!
헌데 생각해보면, 이렇게 무작위로 하는 방식보다 조금 더 스마트한 방식이 있을 것 같습니다.
그래서 등장한 것이 UCB 알고리즘입니다.
greedy 방식에서 ① 번 버튼을 누르는 것을 탐욕적인 선택(greedy selection)이라고 합니다.
동전을 던져 셋 중 다른 하나를 고르는 것 보다는, 좀 더 스마트한 방법을 써보자는 건데요.
어떻게?
$A_t \doteq argmax_a [Q_t(a) + c \sqrt \frac{\ln t}{N_t(a)}]$
이렇게요!
$N_t(a)$는 $t$기 이전까지 $a$가 선택된 총 횟수를 뜻하고,
$\ln t$는 시점을 뜻하는 $t$기에 자연로그를 취한 값을 의미합니다.
$N_t(a)$를 분모에, $\ln t$를 분자에 둠으로써 $a$라는 버튼이 시간이 많이 흘렀는데도 덜 뽑혀봤다면, $c$라는 배수만큼 더 무게를 준다! 라는 전략을 표현하는 것입니다.
요약하자면, UCB 방식은 “아직 안살펴본 녀석을 좀 더 꼼꼼히 살펴볼거야..”
정도로 말할 수 있겠네요.
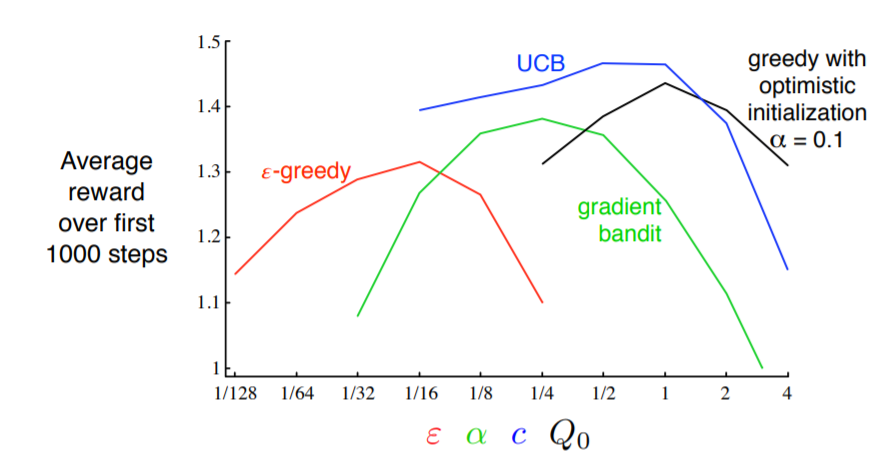
4-4. 그 외 알고리즘
그 외에도 확률적 경사 상승법(Stochastic Gradient Ascent)을 적용한 Gradient Bandit,
Greedy 알고리즘의 초기에 낙천적인 스탠스를 취하게 함으로써 열심히 모든 선택을 탐색하게끔 유도하는 Greedy with optimistic Initialization 등의 알고리즘이 있습니다.
아래의 그림은 알고리즘별 성능 비교 그래프로, 색깔별로 각각 다른 parameter를 의미합니다.
5. 코드 예제
알고리즘을 배웠으니 예제를 살펴봐야죠!
파이썬으로 구현된 multi-armed bandit 알고리즘 라이브러리로는 Bandits, Slots, ContextualBandits 등이 있습니다.
이 외에도, ε-Greedy / UCB / LinUCB / Contextual Bandits / Kernel UCB 알고리즘의 수식과 업데이트 규칙 등을 직접 구현해 친절하고 직관적인 예제를 제공하고 있는 레포지터리가 있어, 한번 살펴보겠습니다.
전체 코드는 아래 커맨드로 git clone해 확인해 주세요.
> git clone https://github.com/akhadangi/Multi-armed-Bandits.git
#===============================
# Epsilon Greedy ...
#===============================
mab = EpsGreedy(10, 0.05)
results_EpsGreedy, chosen_arms_EpsGreedy, cumulative_reward_EpsGreedy = offlineEvaluate(mab, arms, rewards, contexts, 800)
print('EpsGreedy average reward', np.mean(results_EpsGreedy))
#===============================
# UCB ...
#===============================
mab = UCB(10, 1.0)
results_UCB, chosen_arms_UCB, cumulative_reward_UCB = offlineEvaluate(mab, arms, rewards, contexts, 800)
print('UCB average reward', np.mean(results_UCB))
#===============================
# Linear UCB (Contextual) ...
#===============================
mab = LinUCB(10, 10, 1.0)
results_LinUCB, chosen_arms_LinUCB, cumulative_reward_LinUCB = offlineEvaluate(mab, arms, rewards, contexts, 800)
print('LinUCB average reward', np.mean(results_LinUCB))
#===============================
# Plotting results ...
#===============================
plt.figure(figsize=(12,8))
plt.plot(cumulative_reward_LinUCB/np.linspace(1,800,800), label = r"$\alpha=1$ (LinUCB)")
plt.plot(cumulative_reward_UCB/(np.linspace(1,800,800)), label = r"$\rho=1$ (UCB)")
plt.plot(cumulative_reward_EpsGreedy/(np.linspace(1,800,800)), label = r"$\epsilon=0.05$ (greedy)")
plt.legend(bbox_to_anchor=(1.2, 0.5))
plt.xlabel("Rounds")
plt.ylabel(r"$T^{-1}\sum_{t=1}^T\ r_{t,a}$", fontsize='large')
plt.title("Per-round Cumulative Rewards after single simulation")
plt.show()
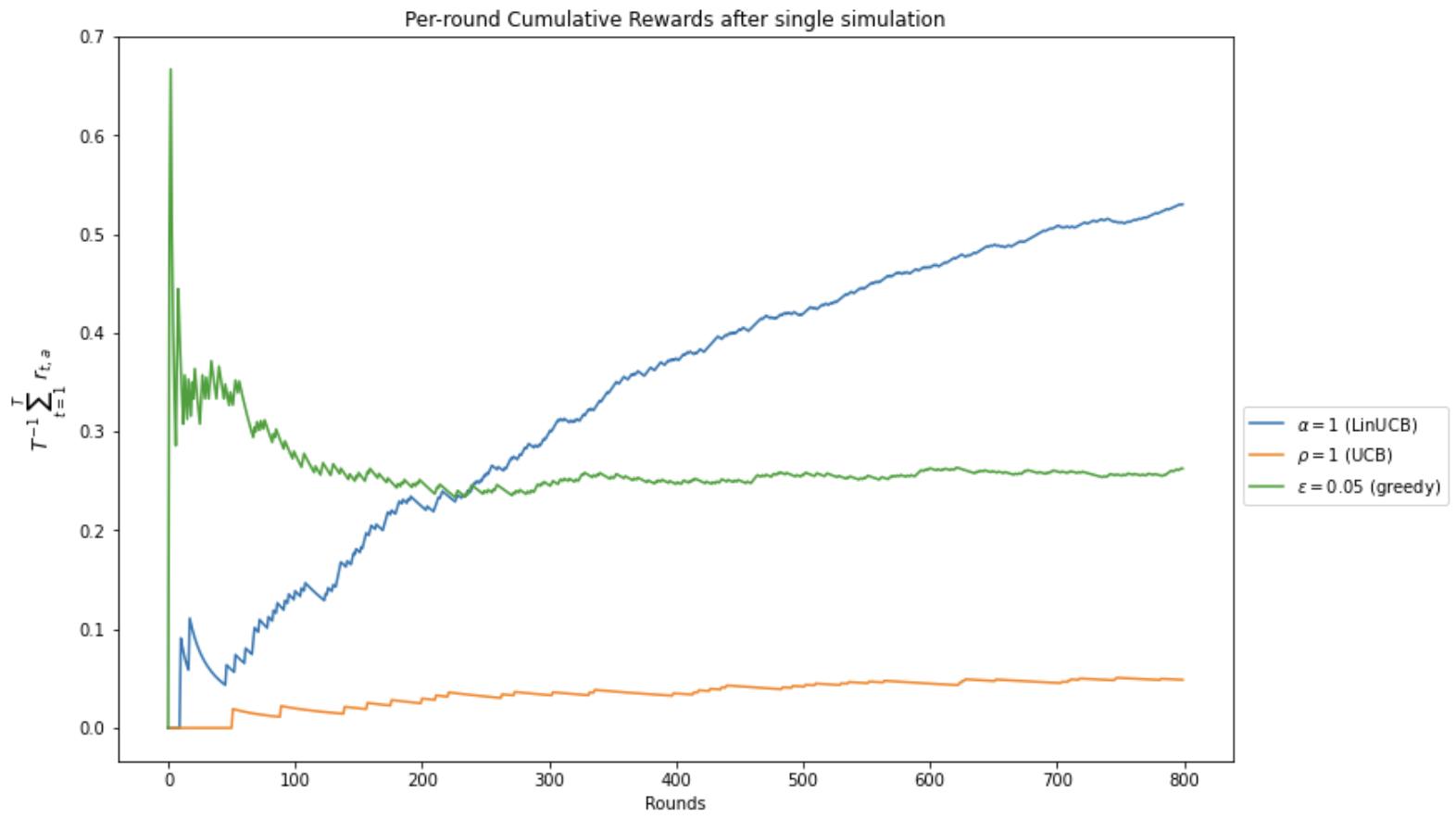
위의 코드는 약 1,000번의 실행동안 LinUCB와 UCB, $\epsilon$이 0.05인 greedy 알고리즘의 실행 결과를 나타냅니다. x축은 앞선 설명에서의 $t$기를 나타냅니다.
여기서 처음 소개된 LinUCB를 간단히 설명하자면, 입력 변수를 활용하는 contextual bandit의 일종으로, 입력된 피처 값을 바탕으로 선형 모델을 적합하여 보상을 예측도록 학습하는 알고리즘입니다. 다음 시간에 이러한 contextual bandits에 대해서도 다루어 보도록 하겠습니다.
개선을 위한 여러분의 피드백과 제안을 코멘트로 공유해 주세요. 내용에 대한 지적, 혹은 질문을 환영합니다.
출처
강화학습 교재 : Reinforcement Learning: An Introduction - by Andrew Barto and Richard S. Sutton

Leave a comment