[General ML Train set] batch 1. MLE와 MAP

MLE(Maximum Likelihood Estimation)와 MAP(Maximum a Posteriori)

파라미터를 추정하는 방법론 중 하나인 MLE와 MAP의 개념에 대해서 알아봅니다.

1. MLE와 MAP는 특정 확률분포, 혹은 머신러닝 모델의 파라미터를 추정하는 방법론이다

2. MLE는 파라미터 $\theta$(theta)가 주어졌을 때 우리가 가진 데이터셋이 발생할 가능성(likelihood)를 극대화하도록 유도하는 파라미터 추정법이다

3. MAP는 사전지식(prior)을 사용하여 우리의 데이터셋(evidence)가 주어졌을 때 사후확률(posterior)를 극대화하는 파라미터 $\theta$를 구하는 파라미터 추정법이다

---

Contents

1. 압정 던지기 예시
2. 이항 분포
3. Maximum Likelihood Estimation
4. MLE 계산하기
5. Simple Error Bound와 PAC learning
6. 사전지식 결합하기, 베이즈 정리
7. Maximum a Posteriori Estimation

압정 던지기 예시

어떤 도박장에서, 압정을 던지는 게임을 하고 있다고 생각해 봅시다. 만약 윗면(뾰족한 면이 위) 혹은 아랫면에 돈을 걸고 맞추면 2배의 돈을 벌게 됩니다.

어떤 갑부가 찾아와서, 우리에게 과학적이고 엔지니어링적인 도움을 요청했다고 해봅시다. 아주 큰 돈을 주면서 말이죠! 갑부의 질문은 다음과 같습니다.

“압정을 던졌을 때 나오는 윗면이 확률은 어떻게되지?!”

이 질문에 답하기 위해, 우리는 아마 몇번 던져보는 시도를 먼저 해볼 것 같습니다.

5번을 던졌더니 3/5가 윗면이 나오고, 2/5가 아랫면이 나왔다고 해 보죠. 이에 따라서 배팅하면 된다고 말해주면 되겠지만, 뭔가 찜찜합니다. 너무 감에 의존하는 것 같지 않나요?

우리가 제시한 답이 정말 해답인지, 그렇다면 어떤 근거로 그 답이 최적이라고 할 수 있는지 한번 알아봅시다.

그 전에, 먼저 알아야 할 몇 가지 개념들이 있습니다.

이항 분포 (Binomial Distribution)

이항 분포는 discrete probability distribution(이산적 확률 분포)의 하나로, 각 시행이 $\theta$의 성공 확률과 1-$\theta$의 실패 확률을 가질 때 $n$개의 독립된 시행을 통해 성공한 횟수가 따르는 분포를 이릅니다.

간단히 말해, 압정 던지기와 같은 실험을 해볼 때, 3/5(앞에서의 $\theta$)의 확률로 윗면이 나올(정의에서의 “성공”) 때, 압정을 100번(정의에서의 n)을 던졌을 경우 윗면이 나온(정의에서의 “성공”) 횟수가 따르는 분포라는 말입니다.

각 시행은 i.i.d (independent and identically distributed) 즉 독립적이고 동일하게 분포되어 있습니다. 다음의 특성을 말합니다.

• independent한 시행: 이전의 압정 던지기가 다음에 영향을 미치지 않음
• identically distributed(베르누이 분포에 따라): 압정의 손상이 없어서 위와 아래가 일정한 확률로 출현함

자, 이제 우리의 압정 던지기 문제로 돌아가 봅시다. 이항 분포를 설명한 것은 압정 던지기라는 시행이 따르는 분포가 이항분포이기 때문이라는 것을 눈치 채셨을 것입니다.

• head가 나올 경우를 승으로 간주하고, 그 확률이 $\theta$ 라고 할 때, $D$(즉 우리가 가진 Dataset)=HHTHT라는 결과가 나왔다고 해 봅시다.
  • 이런 상황이 나올 확률을 계산 해 보면, 다음처럼 정리될 것 같네요. \(\theta^{3}\times (1-\theta )^{2}\)
• 일반화해서 정리하면, 아래처럼 나타낼 수 있겠죠. 여기서 $a_{H}$와 $a_{T}$는 각각 Head와 Tail이 등장한 횟수를 의미합니다. \(P(D|\theta ) = \theta^{a_{H}}\times (1-\theta )^{a_{T}}\)

이런 상황에서, 어떻게하면 head가 나올 확률은 3/5이고 tail의 확률은 2/5라는 결론으로 도달할 수 있을까요?

---

Maximum Likelihood Estimation

지금까지의 이야기를 정리해 보겠습니다.

• 데이터: 관측한 시퀀스 데이터셋 $D$는 $a_{H}$, $a_{T}$로 이루어져 있음. 이 $D$의 예시는 “H,H,T,H,T”를 들 수 있음.
• 우리의 가설: 압정 던지기의 결과는 $\theta$의 이항분포를 따름.

여기서, 우리의 가설을 더욱 강하게 하기 위해서는 어떻게 해야 할까요? 먼저, 이 관측치에 대해 더 나은 분포를 찾아보는 방법이 있겠습니다. 하지만, 둘 중 하나의 결과를 낳는 binomial한 시행을 모델링하는 상황에서는 이항분포를 사용하는 것이 적절해 보입니다.
두 번째로, $\theta$의 가장 적절한 후보군을 만들어 내는 방법이 있겠습니다. 이항분포를 따른다고 가정했을 때 우리가 관측한 데이터의 확률을 최대화하는, 달리 말해 우리가 관측한 현상을 잘 설명해내는, 분포의 파라미터 $\theta$를 찾아낸다면 우리의 가설이 강해질 것 같습니다.

여기서 어떻게 이 $\theta$를 찾아낼 수 있을까요? 그 방법 중 하나가, Maximum Likelihood Estimation(최우추정법, MLE) 을 사용하는 것 입니다. 아래의 수식은 MLE의 추정치를 나타냅니다.

\[\hat{\theta}=argmax_{\theta}P(D|\theta)\]

풀이하자면, 우리의 파라미터 $\theta$(즉 Head가 나올 확률)가 주어졌을 때, 우리가 관측한 데이터 $D$ (가령 H,H,T,H,T)가 발생할 확률을 극대화하는 그 $\theta$를 추정한 녀석이라는 뜻입니다.

이 풀이가 바로 MLE의 정의를 나타냅니다. 모델링하고자 하는 사건에 대해 특정 분포를 가정했을 때, 그 분포의 파라미터가 주어진 경우 관측된 데이터셋 $D$를 가장 그럴싸하게 만들어 주는 $\theta$를 추정하는 방법이라고 정리할 수 있겠습니다.

MLE 계산하기

그렇다면 이 theta를 어떻게 찾을 수 있을까요? 늘 그래왔듯이, 우리는 미분을 사용해 극점을 찾아 optimize할 수 있겠습니다. 아래의 수식을 $\theta$에 대해 미분하여 도함수가 0이 되는 $\theta$를 찾으면, 그 지점이 최적점이라고 생각할 수 있겠습니다.

\[\hat{\theta}=argmax_{\theta}P(D|\theta)=argmax_{\theta}\theta^{a_{H}}(1-\theta )^{a_{T}}\]

그러나 이 식 자체는 그대로 처리하기는 어려울 것 같습니다. 이런 경우, 흔히 단조증가함수인 log를 양변에 취해줍니다. 이 단조증가 함수의 특성 덕분에, log를 취한 뒤 계산하든, 취하지 않고 계산하든 동일한 지점의 $\theta$에서 MLE가 구해집니다.

\[\hat{\theta}=argmax_{\theta}lnP(D|\theta)=argmax_{\theta}ln\{\theta^{a_{H}}(1-\theta )^{a_{T}}\}=argmax_{\theta}\{a_{H}ln\theta+a_{T}ln(1-\theta)\}\]

이를 구하기 위해서는 $argmax$ 안의 식을 $\theta$에 대해 미분하여서 도함수를 0으로 놓고 계산하면 되겠습니다.

• $\frac{\mathrm{d} }{\mathrm{d} x}(a_{H}ln\theta+a_{T}ln(1-\theta))=0$
• $\frac{a_{H}}{\theta}-\frac{a_{T}}{1-\theta}=0$
• $\theta = \frac{a_{H}}{a_{T}+a_{H}}$

결과적으로, $\theta$가 $\frac{a_{H}}{a_{T}+a_{H}}$일 때, 이 $\theta$는 MLE의 관점에서 최적의 후보가 된다는 말입니다. 정리하자면,

\[\hat{\theta} = \frac{a_{H}}{a_{T}+a_{H}}\]

가 됩니다. 이를 우리의 상황에 대입해 볼까요? Head가 등장한 횟수가 $a_{H}$, Tail이 등장한 횟수가 $a_{T}$인데 우리의 데이터 $D$는 “H,H,T,H,T”이므로 $a_{H}=3$이 될 것이고, $a_{T}=2$가 될 것입니다. 이를 그대로 대입하면,

\[\hat{\theta} = \frac{3}{2+3}=\frac{3}{5}\]

즉, 처음에 구했던 $\frac{3}{5}$이 구해진 것이죠!

여기까지 간단한 사례를 들어 MLE를 구해 보았습니다. 그런데, 여기서 시행을 더 늘려보면 어떨까요?
만일 50번의 시행을 해봤더니 Head가 30번이 나왔다고 해봅시다. 이 경우, MLE를 다시 계산해 보면 그대로 $\frac{3}{5}$가 되겠죠. 그럼 아무 소득이 없는걸까요?

그렇지 않습니다. MLE로 추정한 $\hat{\theta}$라는 값은 말 그대로 estimation입니다. 많은 시행을 통해 MLE를 구한다면, 이 추정의 오차를 줄였다고 할 수 있습니다.

Simple Error Bound와 PAC learning

50번 시행해서 도출된 결과와, 5번 시행해서 도출된 결과는 그 값 자체로는 같을지라도 그 값이 주는 신뢰성이 다릅니다.

$\theta^{*}$를, $\epsilon>0$의 에러를 갖는 압정 던지기 시행의 참값(true parameter)라고 해보겠습니다. 여기에 대해, 수학과에서 온 Hoeffding’s inequality에 의해 다소 복잡해 보이는 수식을 simple upper bound로 얻어낼 수 있습니다.

\[P(|\hat{\theta}-\theta^{*}| \geq \epsilon)\leq 2e^{-2N\epsilon^{2}}\]

이 수식을 풀이하자면, $\hat{\theta}$과 $\theta^{*}$의 차이가 특정 error bound보다 클 확률은 시행 횟수 $N$이 커질수록, 또 error bound가 커질수록 작아진다는 의미입니다.

따라서 시행이 늘어났으므로 실제 파라미터 값과 추정된 파라미터의 값의 차이인 오차($\epsilon$)가 더 작아졌을 것이라는 주장을 할 수 있습니다. 달리 말해 여러번 시행한 결과로 얻은 값이 오차가 적다는 말이지요.

이제 역으로, 오차가 0.1이 넘는 확률을 0.01보다 낮게끔 만들 수 있는 N을 구할 수도 있겠습니다. 이러한 과정을 PAC(Probably Approximate Correct) learning이라고 합니다. “0.01의 확률로 0.1이 넘는 오차가 나타날 $\hat{\theta}$이 바로 0.6입니다”라는 식의 진술이 PAC learning의 결과물의 한 예가 되겠습니다.

사전지식 결합하기 (Incorporating prior knowledge)

지금까지 MLE의 관점에서 파라미터를 추정하는 방식을 배워왔습니다. 이와는 다른 관점에서 어떻게 접근해볼 수 있을까요? 이번에는 베이지안적 관점인 MAP를 배워보겠습니다.

지금까지와 마찬가지로, 압정을 던지는 예시를 그대로 가져와 보겠습니다.
MLE로 0.6이라는 $\hat{\theta}$ 값을 구하고 훈훈하게 마무리 지어지던 중, “잠깐!!” 이라 외치며 베이즈라는 사람이 등장합니다.

토마스 베이즈(Thomas Bayes, 1701~1761)

• 베이즈: “회장님, 그거 진짜 0.6맞나요? 50:50 확률 아닙니까?”
• 회장님: “나도 그렇게 생각하긴 했는데…”
• 베이즈: “그럼 그 사전정보를 가미한 $\theta$를 찾아보면 어떨까요?”
• 회장님: “어떻게?”

어떻게 구할 수 있을까요? 우리는 아주 익숙하고 유명한 정리를 떠올려볼 수 있겠습니다.

\[P(\theta|D)=\frac{P(D|\theta)P(\theta)}{P(D)}\]

이 식을 한 번 뜯어볼까요? 좌변의 $P(\theta \vert D)$는, $D$가 주어졌을 때 $\theta$가 사실일 확률을 나타냅니다. 즉, 우리가 알고자하는 사후확률(posterior)이죠.

이 것을 구하기 위해서는, 우리가 가진 $D$의 확률, 그리고 사전지식을 활용해야 합니다. likelihood는 앞서서 이미 정의했었죠.

\[P(D|\theta ) = \theta^{a_{H}}\times (1-\theta )^{a_{T}}\]

여기서 우리의 사전지식이 가미될 수 있습니다. $P(\theta)$가 0.5가 아닐까? 하는 방식으로 우리의 사전지식을 수식에 녹여낼 수 있겠네요.

다시 정리하면, 아래처럼 나타낼 수 있겠습니다.

\[P(Posterior)=\frac{P(Likelihood) \times P(Prior\space Knowledge)}{P(Evidence, \space Normalizing \space Constant)}\]

베이지안 관점에서의 더 많은 공식

앞서서 Evidence 부분이었던 $P(D)$는 이미 주어진 상수이므로 우리의 관심 밖입니다. 따라서 이를 소거하되, 등호를 비례기호로 바꾸어주겠습니다. (참고: 기호 $\propto$는 proportion으로 읽습니다)

\[P(\theta|D) \propto P(D|\theta)P(\theta)\]

또, 다음과 같은 식을 미리 구해 놓았습니다.

\[P(D|\theta ) = \theta^{a_{H}}\times (1-\theta )^{a_{T}}\]

여기서 $P(\theta)$를 잘 나타내 주는 것이 관건이 되겠습니다. 앞에서 나타낸 방식과 유사하게, 특정 분포에 의존해 표현해 주는 것이 필요합니다. 단순히 0.5를 그대로 쓸 수는 없을 테니까요.

여기서 베이즈씨는 베타분포(beta distribution)을 사용할 것을 제안합니다.

베타 분포의 cumulative density function

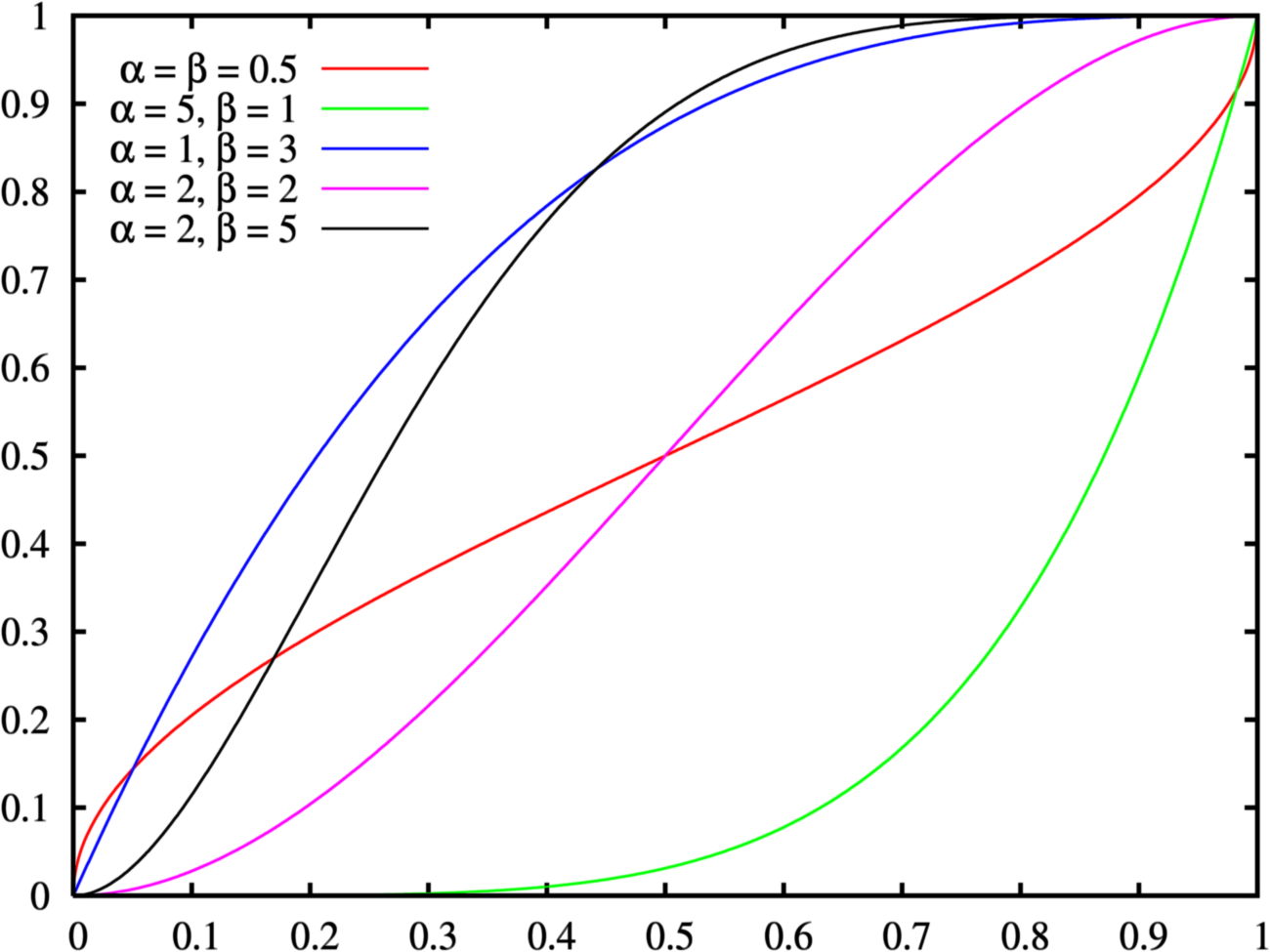
베타 분포란, 아래의 pdf(probability density function)를 갖습니다.

\(P(\theta)={\frac {\theta^{\alpha -1}(1-\theta)^{\beta -1}}{B(\alpha,\beta)}},\) \(B(\alpha,\beta)={\frac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}}, \Gamma(\alpha)=(\alpha - 1)!\)

베타 분포는 0과 1사이에 cdf(cumulative density function)가 confine 되어 있기 때문에, 확률을 나타내기가 용이하다는 특성을 가지고 있습니다. 위의 식이 다소 기괴해 보일 수 있지만, 식 안의 $\alpha와 \beta$는 단순히 앞면이 나오는 횟수와 뒷면이 나오는 횟수로 생각하시면 됩니다. 저 두개의 파라미터를 입력으로 받아 확률값을 나타내는 것이지요.

이제 베타분포를 사용해 수식을 정리해 보겠습니다.

\[P(\theta|D) \propto P(D|\theta)P(\theta) \propto\theta^{\alpha_{H}}(1-\theta)^{\alpha_{T}}\theta^{\alpha-1}(1-\theta)^{\beta-1}\]

식을 살펴보면, $\theta^{\alpha_{H}}(1-\theta)^{\alpha_{T}}$는 베타분포를 나타낸 $P(\theta)$식의 분자부분을 가져왔음을 알 수 있습니다. 분모는 어디 갔냐구요? 어차피 $\theta$에 대해 미분할 것이기 때문에, 분모 부분은 앞에서와 비슷하게 normalizing constant가 되겠죠. 이를 제거해주며 비례식으로 식을 전개해 줍니다.

\[=\theta^{a_{H}+\alpha-1}(1-\theta)^{a_{T}+\beta-1}\]

지수에 대해서 자승으로 처리가 되므로, 위의 식처럼 정리될 수 있습니다. 왠지 봤던 꼴이 또 나온 것 같지 않나요?

Maximum a Posteriori Estimation

• 회장님: “뭐야, 잠만! 내가 원했던 건 앞면이 나올 확률이였어. 사전정보를 더 넣는다더니 어떻게 흘러가고 있는거야?”
• 베이즈: “거의 다 왔습니다!”

마저 정리해 봅시다. 지금까지 아래의 식을 도출해 냈습니다.

\[P(\theta|D) \propto \theta^{a_{H}+\alpha-1}(1-\theta)^{a_{T}+\beta-1}\]

이를 극점을 활용한 최적화를 통해 구해보면(즉 미분해서 구해보면) 아래처럼 정리되겠습니다.

\[\hat{\theta}=\frac{a_{H}+\alpha-1}{a_{H}+\alpha+a_{T}+\beta-2}\]

이 식에 대해서, $\alpha와 \beta$라는 사전지식을 이렇게 저렇게 바꾸어 보면서 최종 결과값인 $\hat{\theta}$값을 0.6이 아닌 다른 값으로 얻어낼 수 있을 것입니다.

---

결론

MLE와 MAP는 각각 이렇게 정리됩니다.

MLE (Maximum Likelihood Estimation) \[\hat{\theta} = \frac{a_{H}}{a_{T}+a_{H}}\]

MAP (Maximum A Posteriori) \[\hat{\theta}=\frac{a_{H}+\alpha-1}{a_{H}+\alpha+a_{T}+\beta-2}\]

이 둘의 차이는 무엇일까요? 간단히 말해, “사전지식을 반영할 것인가, 그렇지 않을 것인가“하는 관점의 차이입니다. 전자의 경우 사전지식이 반영될 여지가 전혀 없는데 반해, 후자에는 $\alpha와 \beta$를 통해 사전지식을 반영할 수 있습니다. 만일 $\alpha와 \beta$를 1로 둔다면 위의 MLE와 MAP는 완전히 동일한 식임을 알 수 있습니다.

또한, 시행이 매우 많아지면, MAP의 식과 MLE의 식은 거의 같아질 것입니다. alpha와 beta라는 파라미터가 가지게 될 영향은 시행이 많아질수록 더욱 약해지겠죠. 단순히 아래와 같은 경우를 생각해 보면 바로 이해할 수 있습니다.

\[\frac{10000}{4000+10000} \approx \frac{10000+\alpha-1}{10000+\alpha+4000+\beta-2}\]

여기서 표본의 수가 매우 적을 때, 실제 상황을 충분히 잘 반영하는 사전지식을 사용한다면 MAP의 접근이 더 좋은 결과를 얻을 수 있으리라 기대해 볼 수 있습니다. 반면에 잘못된 사전지식을 사용하여 가설을 세운다면 치명적인 결과를 낳을 수 있는 것도 MAP의 베이지안적 접근법이 갖는 한계라고 볼 수 있겠죠.

---

닫으며

지금까지 MLE와 MAP의 개념에 대해 알아 보았습니다.

개선을 위한 여러분의 피드백과 제안을 코멘트로 공유해 주세요. 내용에 대한 지적, 혹은 질문을 환영합니다.

해당 포스트는 카이스트 문일철 교수님의 동의를 얻고, 강좌 내용과 자료, 그리고 reference의 자료를 참고하여 작성되었습니다. 원 강좌는 여기에서 보실 수 있습니다.

자료 공유를 허락해 주신 문일철 교수님께 감사의 말씀을 전합니다.